What are some types that discriminate between categories?

Question

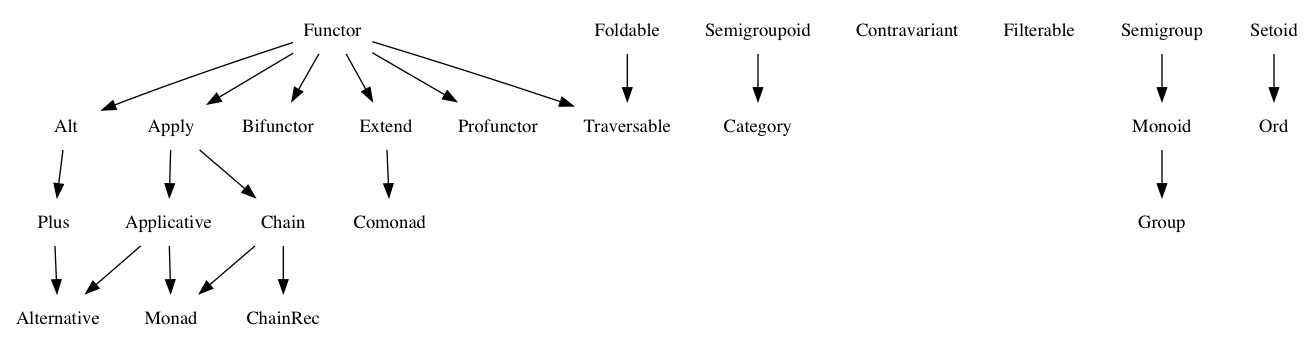
I'm still getting familiar with all this category theory stuff, and just about every example I see is with a Maybe or an Array. But I haven't found any examples that discriminate between these categories. For example, here are some of the questions I've still been unable to answer:

1. whats a Semigroup that isn't also a Monoid?
2. whats a Foldable that isn't also a Traversable? [Duplicate]
3. whats an Functor that isn't also an Apply?
4. whats an Apply that isn't also an Applicative?
5. whats an Apply that isn't also a Chain?
6. whats a Chain that isn't also a Monad?
7. what an Applicative that isn't also a Monad? [Duplicate]

I'm learning this stuff through the context of JavaScript FantasyLand so that's where I'm getting the lingo from -- I understand there are different words for these things.

Answer 1

1. Whats a Semigroup that isn't also a Monoid?

Cactus gives a great example of a semigroup that's not a monoid. Non-empty (finite) lists of any type represent the free semigroup over that type. Another example is Data.Void.Void, which isn't a Monoid because it doesn't have any elements and therefore doesn't have an identity element. Yet another example is the set of positive integers under addition.

3. Whats an Functor that isn't also an Apply?

One Functor that's not an Apply is Handler.

data Handler a where
  Handler :: Exception e => (e -> IO a) -> Handler a

instance Functor Handler where
  fmap f (Handler h) = Handler (\e -> f <$> h e)

Given Handler f :: Handler (a -> b) and Handler g :: Handler a, you have

f :: e1 -> IO (a -> b)
g :: e2 -> IO a

Where e1 and e2 are (possibly different) types of exception. You need to create h :: e3 -> IO b for some exception type e3. There is no really sensible way to do this**.

It seems harder to find Functors that can't be made into law-abiding Apply instances, because Apply has just one law and therefore admits all sorts of weird things that Applicative would reject.

4. Whats an Apply that isn't also an Applicative?

6. What an Applicative that isn't also a Monad?

Map k and IntMap. Also, (,) a and Const a when a is a Semigroup but not a Monoid. Similarly, some other types fit the pattern of accepting a weaker context for Apply and/or Bind than for Applicative or Monad, respectively.

5. Whats an Apply that isn't also a Chain?

ZipList is an Apply but not a Bind. I don't know what a Chain is.

---

** One semi-sensible way might look like this:

data P x y = P x y deriving (Show, Typeable)
instance (Exception x, Exception y) =>
            Exception (P x y)
instance Apply Handler where
  Handler f <.> Handler g =
    Handler (\(P e1 e2) -> f e1 <*> g e2)

I think this obeys the Apply law, but I'm not yet completely certain.

Answer 2

Non-empty lists, defined as data NEList a = Cons a [a] are semigroups but not monoids.