How to fill a fixed rectangle with square pieces entirely?

Question

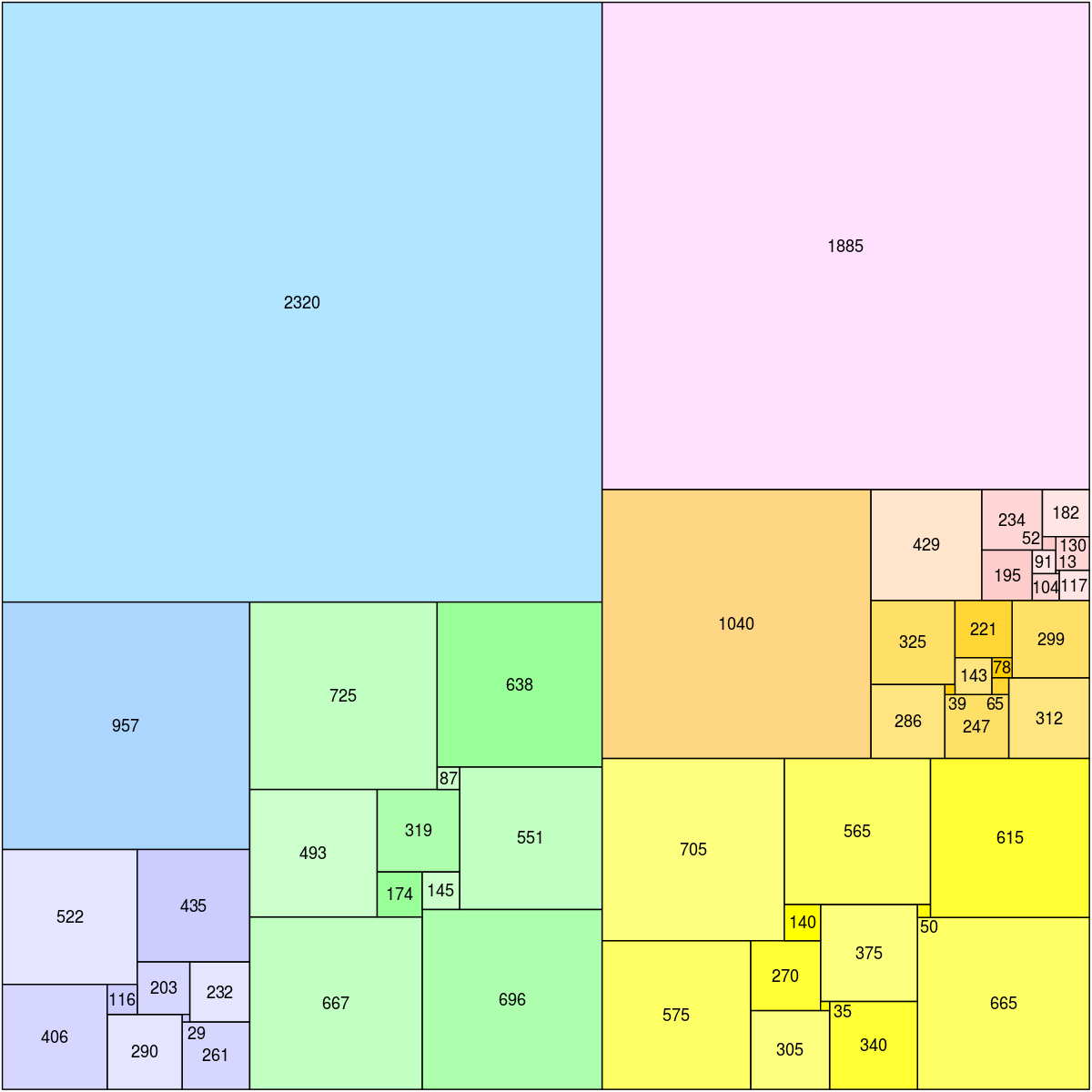
Is this knapsack algorithm or bin packing? I couldn't find an exact solution but basically I have a fixed rectangle area that I want to fill with perfect squares that represents my items where each have a different weight which will influence their size relative to others.

They will be sorted from large to smaller from top left to bottom right.

Also even though I need perfect squares, in the end some non-uniform scaling is allowed to fill the entire space as long as they still retain their relative area, and the non-uniform scaling is done with the least possible amount.

What algorithm I can use to achieve this?

Answer 1

There's a fast approximation algorithm due to Hiroshi Nagamochi and Yuusuke Abe. I implemented it in C++, taking care to obtain a worst-case O(n log n)-time implementation with worst-case recursive depth O(log n). If n ≤ 100, these precautions are probably unnecessary.

#include <algorithm>
#include <iostream>
#include <random>
#include <vector>

namespace {

struct Rectangle {
  double x;
  double y;
  double width;
  double height;
};

Rectangle Slice(Rectangle &r, const double beta) {
  const double alpha = 1 - beta;
  if (r.width > r.height) {
    const double alpha_width = alpha * r.width;
    const double beta_width = beta * r.width;
    r.width = alpha_width;
    return {r.x + alpha_width, r.y, beta_width, r.height};
  }
  const double alpha_height = alpha * r.height;
  const double beta_height = beta * r.height;
  r.height = alpha_height;
  return {r.x, r.y + alpha_height, r.width, beta_height};
}

void LayoutRecursive(const std::vector<double> &reals, const std::size_t begin,
                     std::size_t end, double sum, Rectangle rectangle,
                     std::vector<Rectangle> &dissection) {
  while (end - begin > 1) {
    double suffix_sum = reals[end - 1];
    std::size_t mid = end - 1;
    while (mid > begin + 1 && suffix_sum + reals[mid - 1] <= 2 * sum / 3) {
      suffix_sum += reals[mid - 1];
      mid -= 1;
    }
    LayoutRecursive(reals, mid, end, suffix_sum,
                    Slice(rectangle, suffix_sum / sum), dissection);
    end = mid;
    sum -= suffix_sum;
  }
  dissection.push_back(rectangle);
}

std::vector<Rectangle> Layout(std::vector<double> reals,
                              const Rectangle rectangle) {
  std::sort(reals.begin(), reals.end());
  std::vector<Rectangle> dissection;
  dissection.reserve(reals.size());
  LayoutRecursive(reals, 0, reals.size(),
                  std::accumulate(reals.begin(), reals.end(), double{0}),
                  rectangle, dissection);
  return dissection;
}

std::vector<double> RandomReals(const std::size_t n) {
  std::vector<double> reals(n);
  std::exponential_distribution<> dist;
  std::default_random_engine gen;
  for (double &real : reals) {
    real = dist(gen);
  }
  return reals;
}

} // namespace

int main() {
  const std::vector<Rectangle> dissection =
      Layout(RandomReals(100), {72, 72, 6.5 * 72, 9 * 72});
  std::cout << "%!PS\n";
  for (const Rectangle &r : dissection) {
    std::cout << r.x << " " << r.y << " " << r.width << " " << r.height
              << " rectstroke\n";
  }
  std::cout << "showpage\n";
}