Finding out nth fibonacci number for very large 'n'

Question

I was wondering about how can one find the nth term of fibonacci sequence for a very large value of n say, 1000000. Using the grade-school recurrence equation fib(n)=fib(n-1)+fib(n-2), it takes 2-3 min to find the 50th term!

After googling, I came to know about Binet's formula but it is not appropriate for values of n>79 as it is said here

Is there an algorithm to do so just like we have for finding prime numbers?

Answer 1

You can use the matrix exponentiation method (linear recurrence method). You can find detailed explanation and procedure in this blog. Run time is O(log n).

I don't think there is a better way of doing this.

Answer 2

You can save a lot time by use of memoization. For example, compare the following two versions (in JavaScript):

Version 1: normal recursion

var fib = function(n) {   return n < 2 ? n : fib(n - 1) + fib(n - 2); }; 

Version 2: memoization

A. take use of underscore library

var fib2 = _.memoize(function(n) {   return n < 2 ? n : fib2(n - 1) + fib2(n - 2); }); 

B. library-free

var fib3 = (function(){     var memo = {};     return function(n) {         if (memo[n]) {return memo[n];}         return memo[n] = (n <= 2) ? 1 : fib3(n-2) + fib3(n-1);     }; })(); 

The first version takes over 3 minutes for n = 50 (on Chrome), while the second only takes less than 5ms! You can check this in the jsFiddle.

It's not that surprising if we know version 1's time complexity is exponential (O(2^N/2)), while version 2's is linear (O(N)).

Version 3: matrix multiplication

Furthermore, we can even cut down the time complexity to O(log(N)) by computing the multiplication of N matrices.

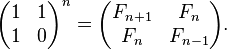
where F_n denotes the nth term of Fibonacci sequence.