What's wrong with following foldl implementation?

Question

By the task we've had to implement foldl by foldr. By comparing both function signatures and foldl implementation I came with the following solution:

myFoldl :: (a -> b -> a) -> a -> [b] -> a
myFoldl _ acc [] = acc
myFoldl fn acc (x:xs) = foldr fn' (fn' x acc) xs
    where
    fn' = flip fn

Just flip function arguments to satisfy foldr expected types and mimic foldl definition by recursively applying passed function. It was a surprise as my teacher rated this answer with zero points.

I even checked this definition stacks its intermediate results in the same way as the standard foldl:

 > myFoldl (\a elm -> concat ["(",a,"+",elm,")"]) "" (map show [1..10])
 > "((((((((((+1)+10)+9)+8)+7)+6)+5)+4)+3)+2)"
 > foldl (\a elm -> concat ["(",a,"+",elm,")"]) "" (map show [1..10])
 > "((((((((((+1)+10)+9)+8)+7)+6)+5)+4)+3)+2)"

The correct answer was the following defintion:

myFoldl :: (a -> b -> a) -> a -> [b] -> a    
myFoldl f z xs = foldr step id xs z
    where step x g a = g (f a x)

Just asking why is my previous definition incorrect ?

Answer 1

Essentially, your fold goes in the wrong order. I think you didn't copy your output from foldl correctly; I get the following:

*Main> myFoldl (\ a elem -> concat ["(", a, "+", elem, ")"]) "" (map show [1..10])
"((((((((((+1)+10)+9)+8)+7)+6)+5)+4)+3)+2)"
*Main> foldl (\ a elem -> concat ["(", a, "+", elem, ")"]) "" (map show [1..10])
"((((((((((+1)+2)+3)+4)+5)+6)+7)+8)+9)+10)"

so what happens is that your implementation gets the first element--the base case--correct but then uses foldr for the rest which results in everything else being processed backwards.

There are some nice pictures of the different orders the folds work in on the Haskell wiki:

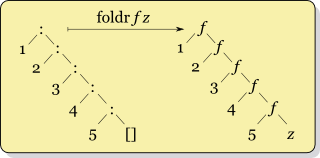
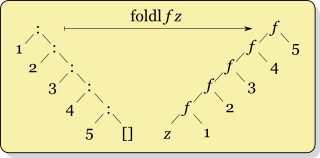
This shows how foldr (:) [] should be the identity for lists and foldl (flip (:)) [] should reverse a list. In your case, all it does is put the first element at the end but leaves everything else in the same order. Here is exactly what I mean:

*Main> foldl (flip (:)) [] [1..10]
[10,9,8,7,6,5,4,3,2,1]
*Main> myFoldl (flip (:)) [] [1..10]
[2,3,4,5,6,7,8,9,10,1]

This brings us to a deeper and far more important point--even in Haskell, just because the types line up does not mean your code works. The Haskell type system is not omnipotent and there are often many--even an infinite number of--functions that satisfy any given type. As a degenerate example, even the following definition of myFoldl type-checks:

myFoldl :: (a -> b -> a) -> a -> [b] -> a
myFoldl _ acc _ = acc

So you have to think about exactly what your function is doing even if the types match. Thinking about things like folds might be confusing for a while, but you'll get used to it.