What kind of algorithm makes a curve like this (img) & can it be done in javascript for flot?

Question

And can you give me an example of an algorithm? alt text http://ryancalderoni.com/archive/ideal_curve.jpg

EDIT: And then how would I calculate the math using Javascript? Can someone add that? Sorry to not include that context originally..

NOTE: I am using 'flot' to graph it and the input for flot is a javascript array like this:

[[x,y],[x,y],[x,y]...]

So given the values that change the curve I output all the points to an array with a loop and spit it out to flot to graph.

Answer 1

A typical sigmoid curve is the tanh(x) curve.

By definition,

  tanh(x) = sinh(x) / cosh(x) =
          = [(1/2) (e^x - e^-x)] / [(1/2) (e^x + e^-x)] =
          = (e^x - e^-x) / (e^x + e^-x) = 
          = (e^(2x) - 1) / (e^(2x) + 1)

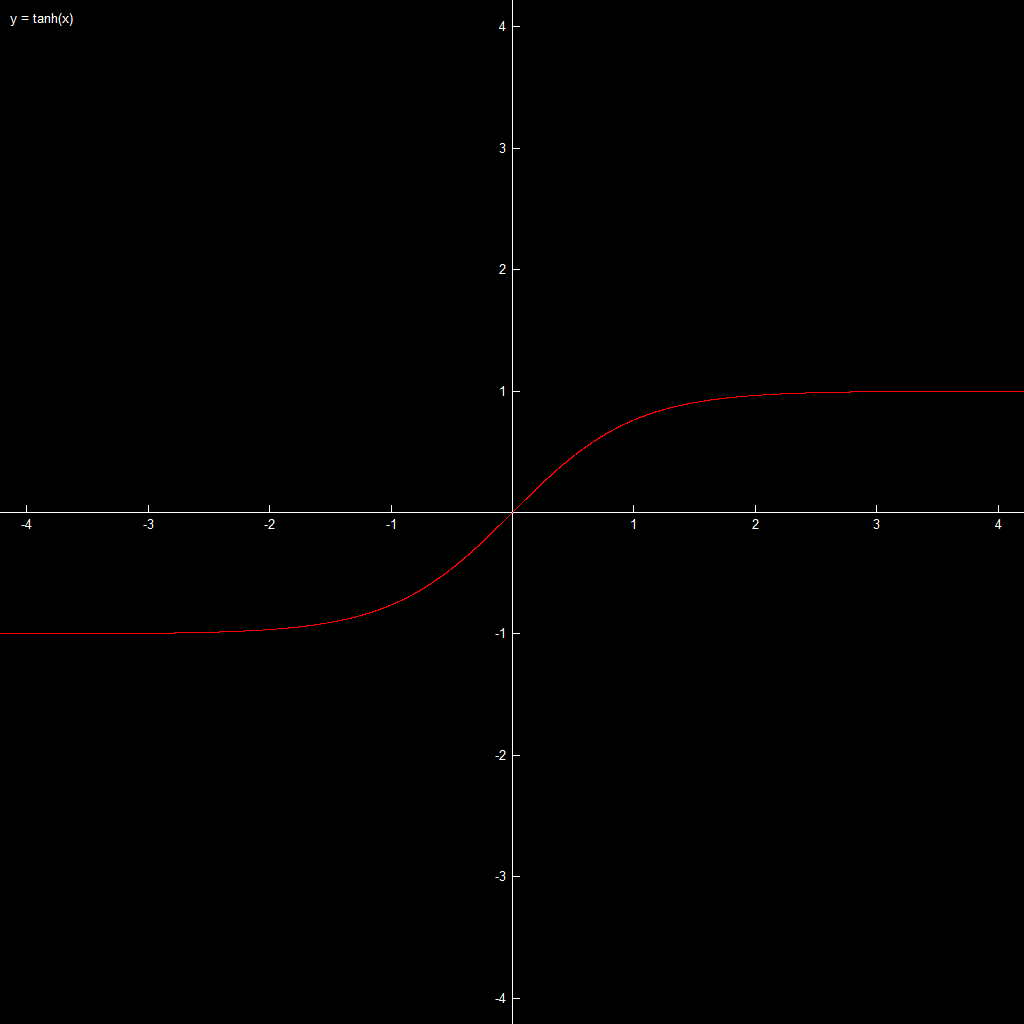
(High-res)

Notice that the lines of symmetry are shifted with respect to your sample picture. To make a tanh graph look more like your example, simply move it up and to the right:

y = 1 + (e^(2x - 6) - 1) / (e^(2x - 6) + 1)

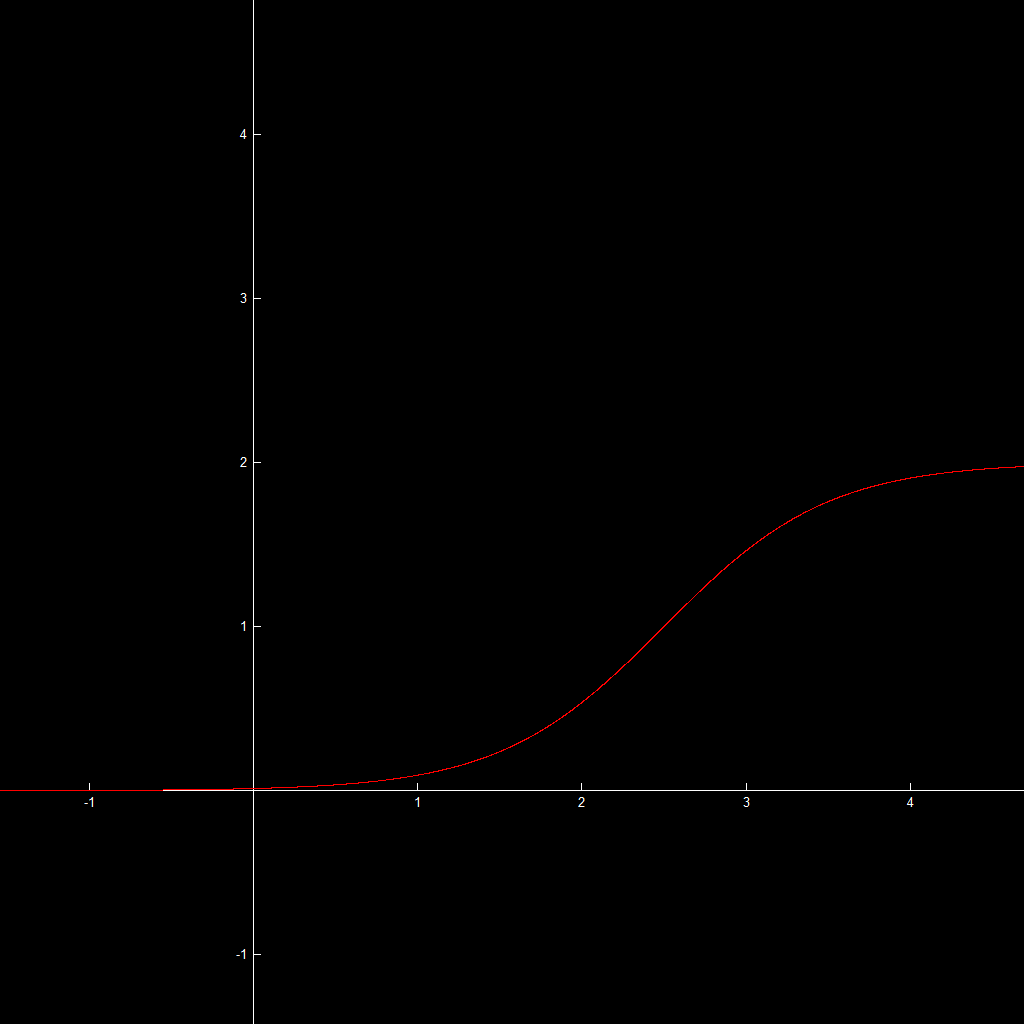
(High-res)

In JavaScript you implement this expression most efficiently as

exp2x = Math.exp(2*x)
y = (exp2x - 1) / (exp2x + 1)

Update (again)

OK, if you want y to range from 0 to 100, and x to range from 0 to 100, than you might want to try

y = 50 + 50*tanh((x−50)/10)

which looks like

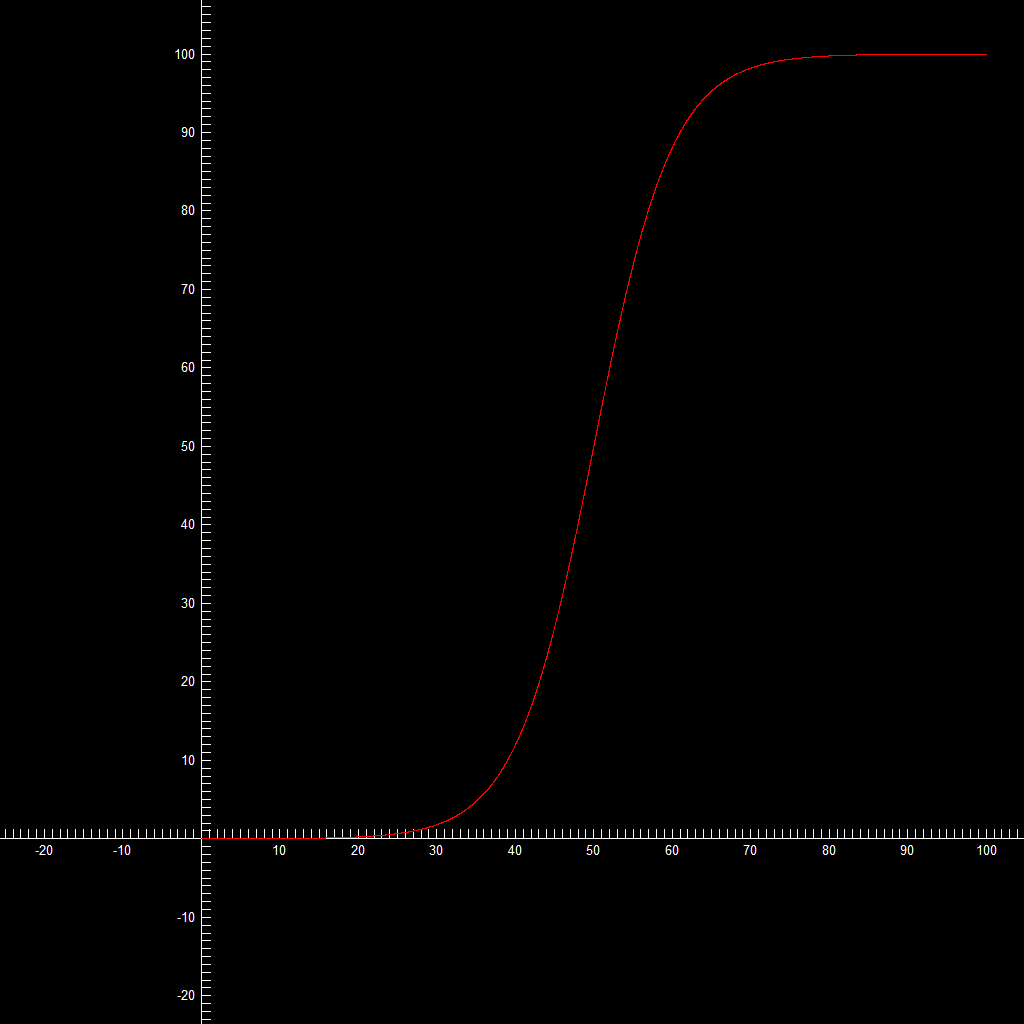
(High-res)

Now

y = 50 + 50 * tanh((x−50)/10)
  = 50 + 50 * (e^((x−50)/5) - 1) / (e^((x−50)/5) + 1)

The error function, erf, looks quite similar, but is much more difficult to compute (unless JavaScript has a built-in erf function).

---

Ryan (OP) adds: implemented!

var y = 50 + 50 * tanh((n-50)/10);

function tanh (arg) {
    return (Math.exp(arg) - Math.exp(-arg)) / (Math.exp(arg) + Math.exp(-arg));
}