Do either of the below approaches use the correct mathematics for rotating a point? If so, which one is correct?
POINT rotate_point(float cx,float cy,float angle,POINT p)
{
float s = sin(angle);
float c = cos(angle);
// translate point back to origin:
p.x -= cx;
p.y -= cy;
// Which One Is Correct:
// This?
float xnew = p.x * c - p.y * s;
float ynew = p.x * s + p.y * c;
// Or This?
float xnew = p.x * c + p.y * s;
float ynew = -p.x * s + p.y * c;
// translate point back:
p.x = xnew + cx;
p.y = ynew + cy;
}
Direction of Rotation: Counterclockwise or clockwise direction. Positive rotations are counterclockwise. Negative rotations are clockwise. For example, to rotate the point (2, 5) counterclockwise about the origin by 90 degrees, we use the rule: (x,y)→(−y,x) ( x , y ) → ( − y , x ) .
90 Degree Rotation When rotating a point 90 degrees counterclockwise about the origin our point A(x,y) becomes A'(-y,x). In other words, switch x and y and make y negative.
From Wikipedia
To carry out a rotation using matrices the point (x, y) to be rotated is written as a vector, then multiplied by a matrix calculated from the angle, θ, like so:

where (x′, y′) are the co-ordinates of the point after rotation, and the formulae for x′ and y′ can be seen to be
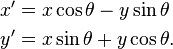
If you love us? You can donate to us via Paypal or buy me a coffee so we can maintain and grow! Thank you!
Donate Us With