O(N log N) Complexity - Similar to linear?

Question

So I think I'm going to get buried for asking such a trivial question but I'm a little confused about something.

I have implemented quicksort in Java and C and I was doing some basic comparissons. The graph came out as two straight lines, with the C being 4ms faster than the Java counterpart over 100,000 random integers.

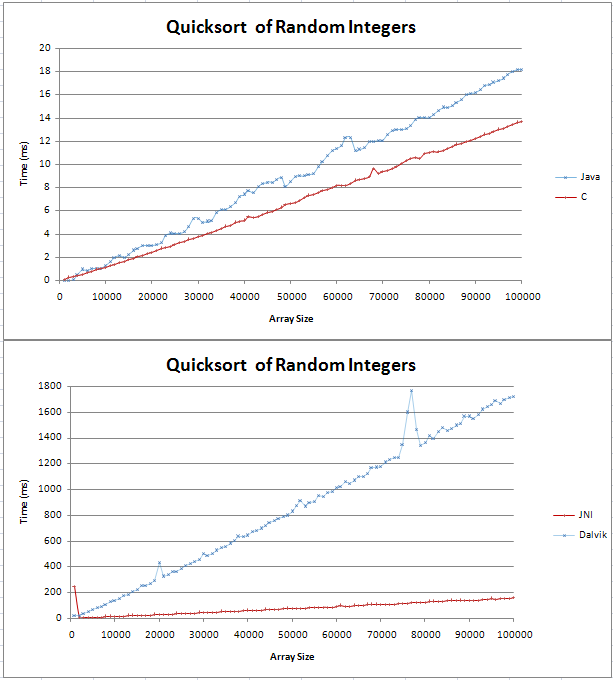
The code for my tests can be found here;

android-benchmarks

I wasn't sure what an (n log n) line would look like but I didn't think it would be straight. I just wanted to check that this is the expected result and that I shouldn't try to find an error in my code.

I stuck the formula into excel and for base 10 it seems to be a straight line with a kink at the start. Is this because the difference between log(n) and log(n+1) increases linearly?

Thanks,

Gav

Answer 1

Make the graph bigger and you'll see that O(n logn) isn't quite a straight line. But yes, it is pretty near to linear behaviour. To see why, just take the logarithm of a few very large numbers.

For example (base 10):

log(1000000) = 6 log(1000000000) = 9 … 

So, to sort 1,000,000 numbers, an O(n logn) sorting adds a measly factor 6 (or just a bit more since most sorting algorithms will depend on base 2 logarithms). Not an awful lot.

In fact, this log factor is so extraordinarily small that for most orders of magnitude, established O(n logn) algorithms outperform linear time algorithms. A prominent example is the creation of a suffix array data structure.

A simple case has recently bitten me when I tried to improve a quicksort sorting of short strings by employing radix sort. Turns out, for short strings, this (linear time) radix sort was faster than quicksort, but there was a tipping point for still relatively short strings, since radix sort crucially depends on the length of the strings you sort.