I am trying to find all possible word/tag pairs or other nested combinations with python and its regular expressions.
sent = '(NP (NNP Hoi) (NN Hallo) (NN Hey) (NNP (NN Ciao) (NN Adios)))'
def checkBinary(sentence):
n = re.findall("\([A-Za-z-0-9\s\)\(]*\)", sentence)
print(n)
checkBinary(sent)
Output:
['(NP (NNP Hoi) (NN Hallo) (NN Hey) (NNP (NN Ciao) (NN Adios)))']
looking for:
['(NP (NNP Hoi) (NN Hallo) (NN Hey) (NNP (NN Ciao) (NN Adios)))',
'(NNP Hoi)',
'(NN Hallo)',
'(NN Hey)',
'(NNP (NN Ciao) (NN Adios))',
'(NN Ciao)',
'(NN Adios)']
I think the regex formula could find the nested parenthesis word/tag pairs aswell but it doesn't return them. How should I do this?
it's actually not possible to do this by using regular expressions, because regular expressions express a language defined by a regular grammar that can be solved by a non finite deterministic automaton, where matching is represented by states ; then to match nested parenthesis, you'd need to be able to match an infinite number of parenthesis and then have an automaton with an infinite number of states.
To be able to cope with that, we use what's called a push-down automaton, that is used to define the context free grammar.
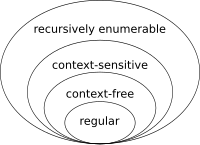
So if your regex does not match nested parenthesis, it's because it's expressing the following automaton and does not match anything on your input:

Play with it
As a reference, please have a look at MIT's courses on the topic:
So one of the ways to parse your string efficiently, is to build a grammar for nested parenthesis (pip install pyparsing first):
>>> import pyparsing
>>> strings = pyparsing.Word(pyparsing.alphanums)
>>> parens = pyparsing.nestedExpr( '(', ')', content=strings)
>>> parens.parseString('(NP (NNP Hoi) (NN Hallo) (NN Hey) (NNP (NN Ciao) (NN Adios)))').asList()
[['NP', ['NNP', 'Hoi'], ['NN', 'Hallo'], ['NN', 'Hey'], ['NNP', ['NN', 'Ciao'], ['NN', 'Adios']]]]
N.B.: there exists a few regular expressions engines that do implement nested parenthesis matching using the push down. The default python re engine is not one of them, but an alternative engine exists, called regex (pip install regex) that can do recursive matching (which makes the re engine context free), cf this code snippet:
>>> import regex
>>> res = regex.search(r'(?<rec>\((?:[^()]++|(?&rec))*\))', '(NP (NNP Hoi) (NN Hallo) (NN Hey) (NNP (NN Ciao) (NN Adios)))')
>>> res.captures('rec')
['(NNP Hoi)', '(NN Hallo)', '(NN Hey)', '(NN Ciao)', '(NN Adios)', '(NNP (NN Ciao) (NN Adios))', '(NP (NNP Hoi) (NN Hallo) (NN Hey) (NNP (NN Ciao) (NN Adios)))']
Regular expressions used in modern languages DO NOT represent regular languages. zmo is right in saying that regular languages in Language Theroy are represented by finite state automata but the regular expressions that use any sort of backtracking like those with capturing groups, lookarounds and etc that are used in modern languages CANNOT be represented by FSAs known in Language Theory. How can you represent a pattern like (\w+)\1 with a DFA or even and NFA?
The regular expression you are looking for can be something like this(only matches to two levels):
(?=(\((?:[^\)\(]*\([^\)]*\)|[^\)\(])*?\)))
I tested this on http://regexhero.net/tester/
The matches are in the captured groups:
1: (NP (NNP Hoi) (NN Hallo) (NN Hey) (NNP (NN Ciao) (NN Adios))
1: (NNP Hoi)
1: (NN Hallo)
1: (NN Hey)
1: (NNP (NN Ciao) (NN Adios))
1: (NN Ciao)
1: (NN Adios)
If you love us? You can donate to us via Paypal or buy me a coffee so we can maintain and grow! Thank you!
Donate Us With