Given an audio stream, find when a door slams (sound pressure level calculation?)

Question

Not unlike a clap detector ("Clap on! clap clap Clap off! clap clap Clap on, clap off, the Clapper! clap clap ") I need to detect when a door closes. This is in a vehicle, which is easier than a room or household door:

Listen: http://ubasics.com/so/van_driver_door_closing.wav

Look:

It's sampling at 16bits 4khz, and I'd like to avoid lots of processing or storage of samples.

When you look at it in audacity or another waveform tool it's quite distinctive, and almost always clips due to the increase in sound pressure in the vehicle - even when the windows and other doors are open:

Listen: http://ubasics.com/so/van_driverdoorclosing_slidingdoorsopen_windowsopen_engineon.wav

Look:

I expect there's a relatively simple algorithm that would take readings at 4kHz, 8 bits, and keep track of the 'steady state'. When the algorithm detects a significant increase in the sound level it would mark the spot.

• What are your thoughts?
• How would you detect this event?
• Are there code examples of sound pressure level calculations that might help?
• Can I get away with less frequent sampling (1kHz or even slower?)

Update: Playing with Octave (open source numerical analysis - similar to Matlab) and seeing if the root mean square will give me what I need (which results in something very similar to the SPL)

Update2: Computing the RMS finds the door close easily in the simple case:

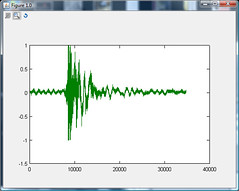
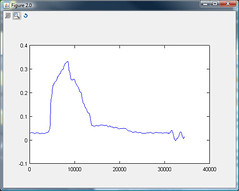
Now I just need to look at the difficult cases (radio on, heat/air on high, etc). The CFAR looks really interesting - I know I'm going to have to use an adaptive algorithm, and CFAR certainly fits the bill.

-Adam

Answer 1

Looking at the screenshots of the source audio files, one simple way to detect a change in sound level would be to do a numerical integration of the samples to find out the "energy" of the wave at a specific time.

A rough algorithm would be:

1. Divide the samples up into sections
2. Calculate the energy of each section
3. Take the ratio of the energies between the previous window and the current window
4. If the ratio exceeds some threshold, determine that there was a sudden loud noise.

Pseudocode

samples = load_audio_samples()     // Array containing audio samples
WINDOW_SIZE = 1000                 // Sample window of 1000 samples (example)

for (i = 0; i < samples.length; i += WINDOW_SIZE):
    // Perform a numerical integration of the current window using simple
    // addition of current sample to a sum.
    for (j = 0; j < WINDOW_SIZE; j++):
        energy += samples[i+j]

    // Take ratio of energies of last window and current window, and see
    // if there is a big difference in the energies. If so, there is a
    // sudden loud noise.
    if (energy / last_energy > THRESHOLD):
        sudden_sound_detected()

    last_energy = energy
    energy = 0;

I should add a disclaimer that I haven't tried this.

This way should be possible to be performed without having the samples all recorded first. As long as there is buffer of some length (WINDOW_SIZE in the example), a numerical integration can be performed to calculate the energy of the section of sound. This does mean however, that there will be a delay in the processing, dependent on the length of the WINDOW_SIZE. Determining a good length for a section of sound is another concern.

How to Split into Sections

In the first audio file, it appears that the duration of the sound of the door closing is 0.25 seconds, so the window used for numerical integration should probably be at most half of that, or even more like　a tenth, so the difference between the silence and sudden sound can be noticed, even if the window is overlapping between the silent section and the noise section.

For example, if the integration window was 0.5 seconds, and the first window was covering the 0.25 seconds of silence and 0.25 seconds of door closing, and the second window was covering 0.25 seconds of door closing and 0.25 seconds of silence, it may appear that the two sections of sound has the same level of noise, therefore, not triggering the sound detection. I imagine having a short window would alleviate this problem somewhat.

However, having a window that is too short will mean that the rise in the sound may not fully fit into one window, and it may apppear that there is little difference in energy between the adjacent sections, which can cause the sound to be missed.

I believe the WINDOW_SIZE and THRESHOLD are both going to have to be determined empirically for the sound which is going to be detected.

For the sake of determining how many samples that this algorithm will need to keep in memory, let's say, the WINDOW_SIZE is 1/10 of the sound of the door closing, which is about 0.025 second. At a sampling rate of 4 kHz, that is 100 samples. That seems to be not too much of a memory requirement. Using 16-bit samples that's 200 bytes.

Advantages / Disadvantages

The advantage of this method is that processing can be performed with simple integer arithmetic if the source audio is fed in as integers. The catch is, as mentioned already, that real-time processing will have a delay, depending on the size of the section that is integrated.

There are a couple of problems that I can think of to this approach:

1. If the background noise is too loud, the difference in energy between the background noise and the door closing will not be easily distinguished, and it may not be able to detect the door closing.
2. Any abrupt noise, such as a clap, could be regarded as the door is closing.

Perhaps, combining the suggestions in the other answers, such as trying to analyze the frequency signature of the door closing using Fourier analysis, which would require more processing but would make it less prone to error.

It's probably going to take some experimentation before finding a way to solve this problem.

Answer 2

You should tap in to the door close switches in the car. Trying to do this with sound analysis is overengineering.

There are a lot of suggestions about different signal processing approaches to take, but really, by the time you learn about detection theory, build an embedded signal processing board, learn the processing architecture for the chip you chose, attempt an algorithm, debug it, and then tune it for the car you want to use it on (and then re-tune and re-debug it for every other car), you will be wishing you just stickey taped a reed switch inside the car and hotglued a magnet to the door.

Not that it's not an interesting problem to solve for the dsp experts, but from the way you're asking this question, it's clear that sound processing isn't the route you want to take. It will just be such a nightmare to make it work right.

Also, the clapper is just an high pass filter fed into a threshold detector. (plus a timer to make sure 2 claps quickly enough together)