Find the paths between two given nodes?

Question

Say I have nodes connected in the below fashion, how do I arrive at the number of paths that exist between given points, and path details?

1,2 //node 1 and 2 are connected 2,3 2,5 4,2 5,11 11,12 6,7 5,6 3,6 6,8 8,10 8,9 

Find the paths from 1 to 7:

Answer: 2 paths found and they are

1,2,3,6,7 1,2,5,6,7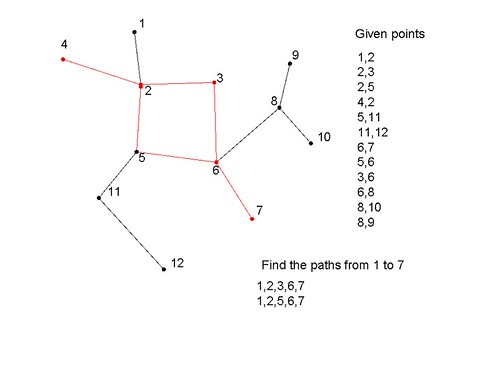 

implementation found here is nice I am going to use the same

Here is the snippet from the above link in python

# a sample graph graph = {'A': ['B', 'C','E'],              'B': ['A','C', 'D'],              'C': ['D'],              'D': ['C'],              'E': ['F','D'],              'F': ['C']}  class MyQUEUE: # just an implementation of a queue      def __init__(self):         self.holder = []      def enqueue(self,val):         self.holder.append(val)      def dequeue(self):         val = None         try:             val = self.holder[0]             if len(self.holder) == 1:                 self.holder = []             else:                 self.holder = self.holder[1:]            except:             pass          return val        def IsEmpty(self):         result = False         if len(self.holder) == 0:             result = True         return result   path_queue = MyQUEUE() # now we make a queue   def BFS(graph,start,end,q):      temp_path = [start]      q.enqueue(temp_path)      while q.IsEmpty() == False:         tmp_path = q.dequeue()         last_node = tmp_path[len(tmp_path)-1]         print tmp_path         if last_node == end:             print "VALID_PATH : ",tmp_path         for link_node in graph[last_node]:             if link_node not in tmp_path:                 #new_path = []                 new_path = tmp_path + [link_node]                 q.enqueue(new_path)  BFS(graph,"A","D",path_queue)  -------------results------------------- ['A'] ['A', 'B'] ['A', 'C'] ['A', 'E'] ['A', 'B', 'C'] ['A', 'B', 'D'] VALID_PATH :  ['A', 'B', 'D'] ['A', 'C', 'D'] VALID_PATH :  ['A', 'C', 'D'] ['A', 'E', 'F'] ['A', 'E', 'D'] VALID_PATH :  ['A', 'E', 'D'] ['A', 'B', 'C', 'D'] VALID_PATH :  ['A', 'B', 'C', 'D'] ['A', 'E', 'F', 'C'] ['A', 'E', 'F', 'C', 'D'] VALID_PATH :  ['A', 'E', 'F', 'C', 'D'] 

Answer 1

Breadth-first search traverses a graph and in fact finds all paths from a starting node. Usually, BFS doesn't keep all paths, however. Instead, it updates a prededecessor function π to save the shortest path. You can easily modify the algorithm so that π(n) doesn't only store one predecessor but a list of possible predecessors.

Then all possible paths are encoded in this function, and by traversing π recursively you get all possible path combinations.

One good pseudocode which uses this notation can be found in Introduction to Algorithms by Cormen et al. and has subsequently been used in many University scripts on the subject. A Google search for “BFS pseudocode predecessor π” uproots this hit on Stack Exchange.