Question: How do you fit a curve to points on a plane if they aren't single valued?
For the example shown, how would one fit a curve (like the black one) to the noisy blue data? It's similar to spline smoothing, but I don't know the order of the data.
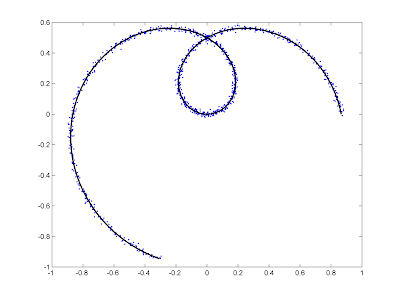
Matlab would be preferred, but pseudocode is fine. Or a pointer to what the correct terminology for this problem is would be great.
Thanks
The curve follows equation A42 with a = 5, b = -1, c = -5 and d = 1. The Trendline type is Polynomial. The highest-order polynomial that Trendline can use as a fitting function is a regular polynomial of order six, i.e., y = ax6 + bx5 +cx4 + ak3 + ex2 +fx + g. polynomials such as y = ax2 + bx3'2 + cx + + e.
Despite its name, you can fit curves using linear regression. The most common method is to include polynomial terms in the linear model. Polynomial terms are independent variables that you raise to a power, such as squared or cubed terms.
The most common way to fit curves to the data using linear regression is to include polynomial terms, such as squared or cubed predictors. Typically, you choose the model order by the number of bends you need in your line. Each increase in the exponent produces one more bend in the curved fitted line.
Your data look like a two-dimensional parametric plot of (x,y) as a function of some underlying parameter t. As such, it may be possible to do a least-squares fit of x(t) and y(t) if you can come up with a reasonable model for them. Your data appear to describe a limacon.
If you love us? You can donate to us via Paypal or buy me a coffee so we can maintain and grow! Thank you!
Donate Us With