Bilinear image interpolation / scaling - A calculation example

Question

I would like to ask you about some bilinear interpolation / scaling details. Let's assume that we have this matrix:

|100 | 50 |
|70  | 20 |

This is a 2 x 2 grayscale image. Now, I would like scale it by factor of two and my matrix looks like this:

| 100   | f1 | 50 | f2 |
| f3    | f4 | f5 | f6 |
| 70    | f7 | 20 | f8 |

so if we would like to calculate f4, the calculation is defined as

f1 = 100 + 0.5(50 - 100) = 75
f7 = 70 +  0.5(20 - 70) = 45

and now finally:

f4 = 75 + 0.5(45 - 75) = 60

However, I can't really understand what calculations are proper for f3 or f1

Do we do the bilinear scaling in each direction separately? Therefore, this would mean that:

f3 = 100 + 0.5(70 - 100) = 85
f1 = 100 + 0.5(50 - 100) = 75

Also, how should I treat f2, f6, f8. Are those points simply being copied like in the nearest neighbor algorithm?

Answer 1

I would like to point you to this very insightful graphic from Wikipedia that illustrates how to do bilinear interpolation for one point:

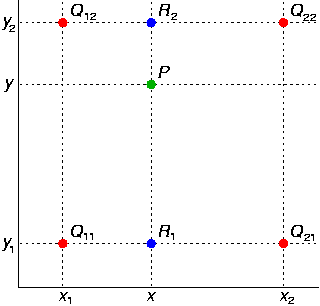
^{Source: Wikipedia}

As you can see, the four red points are what is known. These points you know before hand and P is the point we wish to interpolate. As such, we have to do two steps (as you have indicated in your post). To handle the x coordinate (horizontal), we must calculate what the interpolated value is row wise for the top row of red points and the bottom row of red points. This results in the two blue points R1 and R2. To handle the y coordinate (vertical), we use the two blue points and interpolate vertically to get the final P point.

When you resize an image, even though we don't visually see what I'm about to say, but imagine that this image is a 3D signal f. Each point in the matrix is in fact a 3D coordinate where the column location is the x value, the row location is the y value and the z value is the quantity / grayscale value of the matrix itself. Therefore, doing z = f(x,y) is the value of the matrix at location (x,y) in the matrix. In our case, because you're dealing with images, each value of (x,y) are integers that go from 1 up to as many rows/columns as we have depending on what dimension you're looking at.

Therefore, given the coordinate you want to interpolate at (x,y), and given the red coordinates in the image above, which we call them x1,y1,x2,y2 as per the diagram - specifically going with the convention of the diagram and referencing how images are accessed: x1 = 1, x2 = 2, y1 = 2, y2 = 1, the blue coordinates R1 and R2 are computed via 1D interpolation column wise using the same row both points coincide on:

R1 = f(x1,y1) + (x - x1)/(x2 - x1)*(f(x2,y1) - f(x1,y1))
R2 = f(x1,y2) + (x - x1)/(x2 - x1)*(f(x2,y2) - f(x1,y2))

It's important to note that (x - x1) / (x2 - x1) is a weight / proportion of how much of a mix the output consists of between the two values seen at f(x1,y1) and f(x2,y1) for R1 or f(x1,y2) and f(x2,y2) for R2. Specifically, x1 is the starting point and (x2 - x1) is the difference in x values. You can verify that substituting x1 as x gives us 0 while x2 as x gives us 1. This weight fluctuates between [0,1] which is required for the calculations to work.

It should be noted that the origin of the image is at the top-left corner, and so (1,1) is at the top-left corner. Once you find R1 and R2, we can find P by interpolating row wise:

P = R2 + (y - y2)/(y2 - y1)*(R1 - R2)

Again, (y - y2) / (y2 - y1) denote the proportion / mix of how much R1 and R2 contribute to the final output P. As such, you calculated f5 correctly because you used four known points: The top left is 100, top right is 50, bottom left is 70 and bottom right is 20. Specifically, if you want to compute f5, this means that (x,y) = (1.5,1.5) because we're halfway in between the 100 and 50 due to the fact that you're scaling the image by two. If you plug in these values into the above computation, you will get the value of 60 as you expected. The weights for both calculations will also result in 0.5, which is what you got in your calculations and that's what we expect.

If you compute f1, this corresponds to (x,y) = (1.5,1) and if you substitute this into the above equation, you will see that (y - y2)/(y2 - y1) gives you 0 or the weight is 0, and so what is computed is just R2, corresponding to the linear interpolation along the top row only. Similarly, if we computed f7, this means we want to interpolate at (x,y) = (1.5,2). In this case, you will see that (y - y2) / (y2 - y1) is 1 or the weight is 1 and so P = R2 + (R1 - R2), which simplifies to R1 and is the linear interpolation along the bottom row only.

Now there's the case of f3 and f5. Those both correspond to (x,y) = (1,1.5) and (x,y) = (2,1.5) respectively. Substituting these values in for R1 and R2 and P for both cases give:

f3

R1 = f(1,2) + (1 - 1)/(2 - 1)*(f(2,2) - f(1,2)) = f(1,2)
R2 = f(1,1) + (1 - 1)/(2 - 1)*(f(1,2) - f(1,1)) = f(1,1)
P = R1 + (1.5 - 1)*(R1 - R2) = f(1,2) + 0.5*(f(1,2) - f(1,1))

P = 70 + 0.5*(100 - 70) = 85

f5

R1 = f(1,2) + (2 - 1)/(2 - 1)*(f(2,2) - f(1,2)) = f(2,2)
R2 = f(1,1) + (2 - 1)/(2 - 1)*(f(1,2) - f(1,1)) = f(1,2)
P = R1 + (1.5 - 1)*(R1 - R2) = f(2,2) + 0.5*(f(2,2) - f(1,2))

P = 20 + 0.5*(50 - 20) = 35

So what does this tell us? This means that you are interpolating along the y-direction only. This is apparent when we take a look at P. Examining the calculations more thoroughly of P for each of f3 and f5, you see that we are considering values along the vertical direction only.

As such, if you want a definitive answer, f1 and f7 are found by interpolating along the x / column direction only along the same row. f3 and f5 are found by interpolating y / row direction along the same column. f4 uses a mixture of f1 and f7 to compute the final value as you have already seen.

---

To answer your final question, f2, f6 and f8 are filled in based on personal preference. These values are considered to be out of bounds, with the x and y values both being 2.5 and that's outside of our [1,2] grid for (x,y). In MATLAB, the default implementation of this is to fill any values outside of the defined boundaries to be not-a-number (NaN), but sometimes, people extrapolate using linear interpolation, copy the border values, or perform some elaborate padding like symmetric or circular padding. It depends on what situation you're in, but there is no correct and definitive answer on how to fill in f2, f6 and f8 - it all depends on your application and what makes the most sense to you.

---

As a bonus, we can verify that my calculations are correct in MATLAB. We first define a grid of (x,y) points in the [1,2] range, then resize the image so that it's twice as large where we specify a resolution of 0.5 per point rather than 1. I'm going to call your defined matrix A:

A = [100 50; 70 20]; %// Define original matrix
[X,Y] = meshgrid(1:2,1:2); %// Define original grid of points
[X2,Y2] = meshgrid(1:0.5:2.5,1:0.5:2.5) %// Define expanded grid of points
B = interp2(X,Y,A,X2,Y2,'linear'); %// Perform bilinear interpolation

The original (x,y) grid of points looks like:

>> X

X =

     1     2
     1     2

>> Y

Y =

     1     1
     2     2

The expanded grid to expand the size of the matrix by twice as much looks like:

>> X2

X2 =

    1.0000    1.5000    2.0000    2.5000
    1.0000    1.5000    2.0000    2.5000
    1.0000    1.5000    2.0000    2.5000
    1.0000    1.5000    2.0000    2.5000

>> Y2

Y2 =

    1.0000    1.0000    1.0000    1.0000
    1.5000    1.5000    1.5000    1.5000
    2.0000    2.0000    2.0000    2.0000
    2.5000    2.5000    2.5000    2.5000

B is the output using X and Y as the original grid of points and X2 and Y2 are the points we want to interpolate at.

We get:

>> B

B =

   100    75    50   NaN
    85    60    35   NaN
    70    45    20   NaN
   NaN   NaN   NaN   NaN