Algorithm for placing rectangle with certain size into free area in matrix

Question

Problem
I need to place rectangle with size n×m into free area of matrix with size N×M, where N=n*2-1, M=m*2-1. Matrix cell is considered free if it's true, and occupied if it's false. Center cell is always true, and always will be inside rectangle due to rectangle and matrix's sizes.

Additional requirement is that distance between upper left corner of rectangle and center cell must be as minimal as possible.

Example with n=8 and m=5:

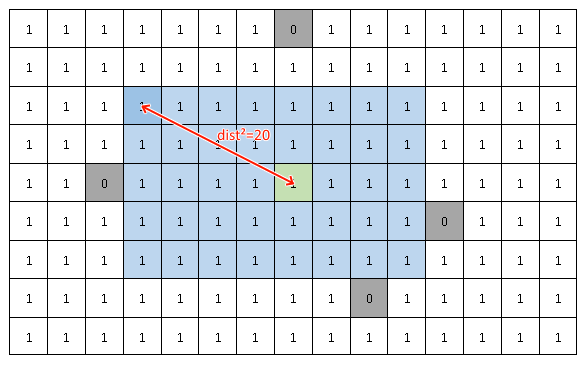
Where gray cells - occupied, green - center cell, blue cells - solution rectangle, red line - distance between upper left corner of rectangle and center cell.

Attempts
Brute force solution would have O(N×M×n×m) time complexity, which is not very optimal. I can eliminate calculations in some cells if I preprocess matrix, but that still would take too much time.

Initially I thought I can take Max Rectangle Problem and just modify condition from max to needed, but it went to dead end (I would need to list all rectangles in a histogram, which I don't know how). Then I thought it's like packing problem, but all I could find was versions of it with initially completely empty space and multiple rectangles, which is not applicable to this problem.

Context
In the past, when user clicks on a grid, my program would place rectangle, with upper left corner coinciding with a click point, if it's empty and fail if it have occupied cells where rectangle would lay. I decided to modify this behavior and instead of failing, find most suitable position for rectangle, while still containing a click point. In matrix pic above, click point is a green cell, and matrix size represents all possible positions of a rectangle.

P.S. I would prefer real language example instead of pseudo-code, if possible. My program is written in Java, but any language is fine.

Answer 1

You can do this in O(N.M) space and time complexity by:

1. Compute the summed area table in O(N.M)
2. Iterate over all top-left corners, check that the summed area in the rectangle is equal to n.m, and update the best position if the distance to the centre has improved. The test is O(1) per top-left corner, and there are O(N.M) top-left corners, so overall O(N.M)

The key idea is that the summed area table allows you to compute the sum of an arbitrary rectangle in O(1) time.