Why is cosine used to calculate the x values and sine the y values for an arc?

Question

I'm trying to understand the math on this raphael.js demo:

http://raphaeljs.com/pie.js

Checkout the sector method:

function sector(cx, cy, r, startAngle, endAngle, params) {
    var x1 = cx + r * Math.cos(-startAngle * rad),
        x2 = cx + r * Math.cos(-endAngle * rad),
        y1 = cy + r * Math.sin(-startAngle * rad),
        y2 = cy + r * Math.sin(-endAngle * rad);
    return paper.path(["M", cx, cy, "L", x1, y1, "A", r, r, 0, +(endAngle - startAngle > 180), 0, x2, y2, "z"]).attr(params);
}

This is the actual demo: http://raphaeljs.com/pie.html

My math is a little rusty and I'm trying to understand the sector function - given the startAngle and endAngle parameters (each start and end point values between 0 and 360 drawing an arc), why does this function work?

Answer 1

Just look at what sin and cos actually mean in a circle:

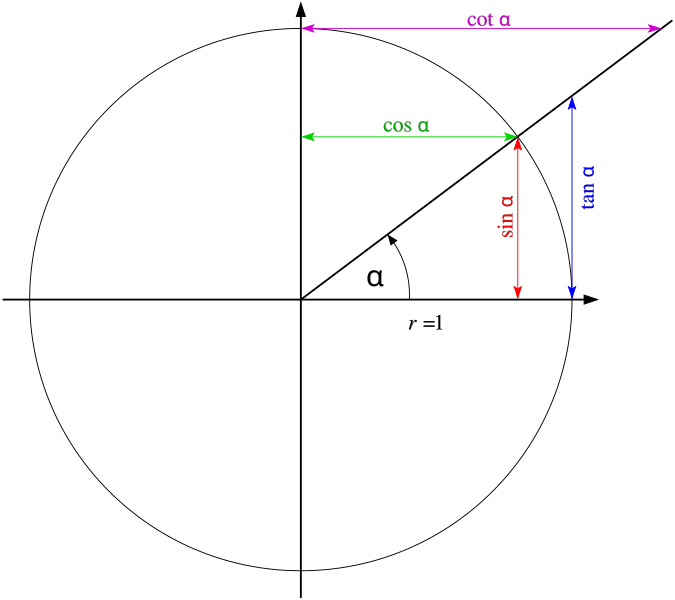
If you have a point on a circle which forms an angle alpha, the cos alpha is the x-part of the point a sin alpha is the y part.

This illustration explains, why the angle is negated.

It means, that you can now specify clockwise angles, which most people with analogue clocks prefer.

Answer 2

It all depends on how you treat startAngle and endAngle. It looks like this is treating them as starting from horizontal to the right (i.e. an angle of 0 is pointing East) and going clockingwise (so an angle of 45 degrees is pointing South-East.

Usually in mathematics we consider angles starting from the horizontal to the right, but increasing anti-clockwise... but if you ask a non-mathematician to draw an angle, they may well treat it from vertically up (i.e. North) increasing clockwise. This looks like it's taking a mixture :) There's no really "wrong" or "right" answer here - it's all a matter of definition.

As pictures are popular, here are the three systems I've described, each assuming the line is of length r:

Normal mathematics: anti-clockwise from x-axis

_{(source: arachsys.com)}

Asking the man on the street to draw an angle (clockwise from y-axis)

The angles used by this code (clockwise from x-axis)

Answer 3

Because arbitrary point on circumference with center (cx, cy) and radius R has the following coordinate (it directly follows from cos and sin geometric definitions - ratio between lengths of corresponding cathetus and hypotenuse):

x = cx + R*cos(a)
y = cy + R*sin(a) for  0 <= a < 2π

So setting limits on angle a you can define arbitrary arc.

Answer 4

If you take 0° as horizontal with x increasing and 90° as vertical with y increasing then as:

cos(0) = 1
sin(0) = 0

cos(90) = 0
sin(90) = 1

you can vary the x value by multiplying it by the cosine and vary the y value by multiplying it by the sine.