Why am I getting dups with random.shuffle in Python?

Question

For a list of 10 ints, there are 10! possible orders or permutations. Why does random.shuffle give duplicates after only 5000 tries?

>>> L = range(10)
>>> rL = list()
>>> for i in range(5000):
...     random.shuffle(L)
...     rL.append(L[:])
... 
>>> rL = [tuple(e) for e in rL]
>>> len(set(rL))
4997
>>> for i,t in enumerate(rL):
...     if rL.count(t) > 1:
...         print i,t
... 
102 (7, 5, 2, 4, 0, 6, 9, 3, 1, 8)
258 (1, 4, 0, 2, 7, 3, 5, 9, 6, 8)
892 (1, 4, 0, 2, 7, 3, 5, 9, 6, 8)
2878 (7, 5, 2, 4, 0, 6, 9, 3, 1, 8)
4123 (5, 8, 0, 1, 7, 3, 2, 4, 6, 9)
4633 (5, 8, 0, 1, 7, 3, 2, 4, 6, 9)
>>> 10*9*8*7*6*5*4*3*2
3628800
>>> 2**19937 - 1
431542479738816264805523551633791983905393 [snip]

>>> L = list()
>>> for i in range(5000):
...     L.append(random.choice(xrange(3628800)))
... 
>>> len(set(L))
4997

Edit: FWIW, if the probability of not having two the same for a single pair is: p = (10! - 1) / 10! and the number of combinations is: C = 5000! / 4998! * 2! = 5000 * 4999 / 2 then the probability of having a duplicate is:

>>> import math
>>> f = math.factorial(10)
>>> p = 1.0*(f-1)/f
>>> C = 5000.0*4999/2
>>> 1 - p**C
0.96806256495611798

Answer 1

It's called the Birthday Paradox.

According to this formula from Wikipedia:

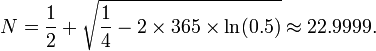
but replacing 365 with 10! you would only need about 2200 examples to have a 50% chance of a collision, and you are way above that.

Answer 2

Because it's... random! If you want all permutations just use itertools.permutations.