When calculating Manhattan Distance, should you calculate distance to end point or start point?

Question

I'm trying to learn the A* algorithm (when applied to a grid pattern) and think I have grasped that before you can find the shortest path, you need to calculate the distance away from the start for any given square.

I'm following the guide here: https://medium.com/@nicholas.w.swift/easy-a-star-pathfinding-7e6689c7f7b2 which has the following image showing the Manhattan distances for each square on the grid:

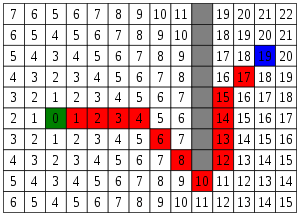
with the start square being the green square and the end being the blue.

However, surely it makes more sense to figure the distance in reverse? The A* chooses the connected square with the shortest distance to the goal right? So surely this (based on the image) would make sense if we started at the end and asked what's the lowest value connected to the start, in this case 17, so go there, then 15 so go there etc etc.

Sub question: The distances in the image away from the start appear to be based on moving through Von Neumann neighbours, so surely on the way back you cannot go diagonally?

Answer 1

F = G + H
F is the total cost of the node.
G is the distance between the current node and the start node.
H is the heuristic — estimated distance from the current node to the end node.

The numbers in the grid represent G (and not the heuristic). G is the actual distance from the start point.
H should be calculated to the endpoint.