Solving the NP-complete problem in XKCD

Question

The problem/comic in question: http://xkcd.com/287/

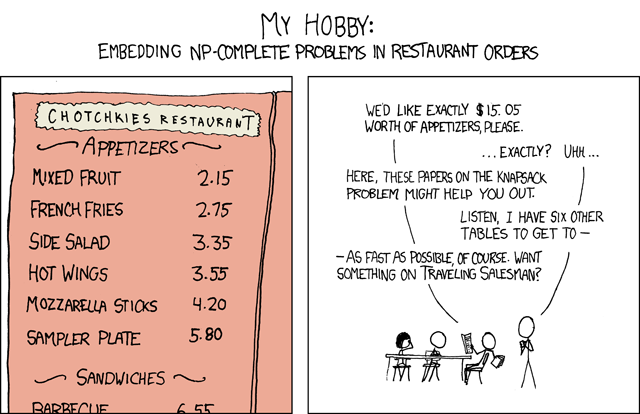
I'm not sure this is the best way to do it, but here's what I've come up with so far. I'm using CFML, but it should be readable by anyone.

<cffunction name="testCombo" returntype="boolean">     <cfargument name="currentCombo" type="string" required="true" />     <cfargument name="currentTotal" type="numeric" required="true" />     <cfargument name="apps" type="array" required="true" />      <cfset var a = 0 />     <cfset var found = false />      <cfloop from="1" to="#arrayLen(arguments.apps)#" index="a">         <cfset arguments.currentCombo = listAppend(arguments.currentCombo, arguments.apps[a].name) />         <cfset arguments.currentTotal = arguments.currentTotal + arguments.apps[a].cost />         <cfif arguments.currentTotal eq 15.05>             <!--- print current combo --->             <cfoutput><strong>#arguments.currentCombo# = 15.05</strong></cfoutput><br />             <cfreturn true />         <cfelseif arguments.currentTotal gt 15.05>             <cfoutput>#arguments.currentCombo# > 15.05 (aborting)</cfoutput><br />             <cfreturn false />         <cfelse>             <!--- less than 15.05 --->             <cfoutput>#arguments.currentCombo# < 15.05 (traversing)</cfoutput><br />             <cfset found = testCombo(arguments.currentCombo, arguments.currentTotal, arguments.apps) />         </cfif>     </cfloop> </cffunction>  <cfset mf = {name="Mixed Fruit", cost=2.15} /> <cfset ff = {name="French Fries", cost=2.75} /> <cfset ss = {name="side salad", cost=3.35} /> <cfset hw = {name="hot wings", cost=3.55} /> <cfset ms = {name="moz sticks", cost=4.20} /> <cfset sp = {name="sampler plate", cost=5.80} /> <cfset apps = [ mf, ff, ss, hw, ms, sp ] />  <cfloop from="1" to="6" index="b">     <cfoutput>#testCombo(apps[b].name, apps[b].cost, apps)#</cfoutput> </cfloop> 

The above code tells me that the only combination that adds up to $15.05 is 7 orders of Mixed Fruit, and it takes 232 executions of my testCombo function to complete.

Is there a better algorithm to come to the correct solution? Did I come to the correct solution?

Answer 1

It gives all the permutations of the solutions, but I think I'm beating everyone else for code size.

item(X) :- member(X,[215, 275, 335, 355, 420, 580]). solution([X|Y], Z) :- item(X), plus(S, X, Z), Z >= 0, solution(Y, S). solution([], 0). 

Solution with swiprolog:

?- solution(X, 1505).  X = [215, 215, 215, 215, 215, 215, 215] ;  X = [215, 355, 355, 580] ;  X = [215, 355, 580, 355] ;  X = [215, 580, 355, 355] ;  X = [355, 215, 355, 580] ;  X = [355, 215, 580, 355] ;  X = [355, 355, 215, 580] ;  X = [355, 355, 580, 215] ;  X = [355, 580, 215, 355] ;  X = [355, 580, 355, 215] ;  X = [580, 215, 355, 355] ;  X = [580, 355, 215, 355] ;  X = [580, 355, 355, 215] ;  No 

Answer 2

The point about an NP-complete problem is not that it's tricky on a small data set, but that the amount of work to solve it grows at a rate greater than polynomial, i.e. there is no O(n^x) algorithm.

If the time complexity is O(n!), as in (I believe) the two problems mentioned above, that is in NP.