Sample uniformly at random from an n-dimensional unit simplex

Question

Sampling uniformly at random from an n-dimensional unit simplex is the fancy way to say that you want n random numbers such that

• they are all non-negative,
• they sum to one, and
• every possible vector of n non-negative numbers that sum to one are equally likely.

In the n=2 case you want to sample uniformly from the segment of the line x+y=1 (ie, y=1-x) that is in the positive quadrant. In the n=3 case you're sampling from the triangle-shaped part of the plane x+y+z=1 that is in the positive octant of R3:

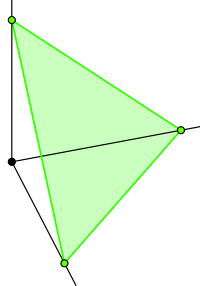
(Image from http://en.wikipedia.org/wiki/Simplex.)

Note that picking n uniform random numbers and then normalizing them so they sum to one does not work. You end up with a bias towards less extreme numbers.

Similarly, picking n-1 uniform random numbers and then taking the nth to be one minus the sum of them also introduces bias.

Wikipedia gives two algorithms to do this correctly: http://en.wikipedia.org/wiki/Simplex#Random_sampling (Though the second one currently claims to only be correct in practice, not in theory. I'm hoping to clean that up or clarify it when I understand this better. I initially stuck in a "WARNING: such-and-such paper claims the following is wrong" on that Wikipedia page and someone else turned it into the "works only in practice" caveat.)

Finally, the question: What do you consider the best implementation of simplex sampling in Mathematica (preferably with empirical confirmation that it's correct)?

Related questions

• Generating a probability distribution
• java random percentages

Answer 1

This code can work:

samples[n_] := Differences[Join[{0}, Sort[RandomReal[Range[0, 1], n - 1]], {1}]]

Basically you just choose n - 1 places on the interval [0,1] to split it up then take the size of each of the pieces using Differences.

A quick run of Timing on this shows that it's a little faster than Janus's first answer.

Answer 2

After a little digging around, I found this page which gives a nice implementation of the Dirichlet Distribution. From there it seems like it would be pretty simple to follow Wikipedia's method 1. This seems like the best way to do it.

As a test:

In[14]:= RandomReal[DirichletDistribution[{1,1}],WorkingPrecision->25]
Out[14]= {0.8428995243540368880268079,0.1571004756459631119731921}
In[15]:= Total[%]
Out[15]= 1.000000000000000000000000

A plot of 100 samples:

alt text http://www.public.iastate.edu/~zdavkeos/simplex-sample.png