Red-Black Tree - Black Height restriction

Question

I was reading wiki about Red-Black Trees.

Can someone elaborate on the 5th restriction:

1. A node is either red or black.

2. The root is black.

3. All leaves (NIL) are black. (All leaves are same color as the root.)

4. Both children of every red node are black.

5. Every simple path from a given node to any of its descendant leaves contains the same number of black nodes.

I'm having difficulties understanding it since given the state of the example RBT after the final case of insertion (case 5 on wiki) gives us:

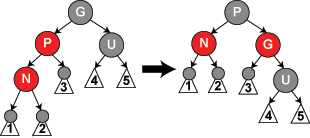
Doesn't 4 and 5 have one more black node than 1,2, and 3?

Answer 1

1, 2, 3, 4 and 5 are all subtrees. We know the colour of the root node in trees 1, 2 and 3 to be black. We do not know whether any of the nodes 1-5 are leaf nodes, because this case of insertion may have been called recursively on some N that was the grandparent of the newly inserted node (from insertion case 3).

Before and after the rotation, subtrees 1, 2 and 3 are all below one black node (G before, P after), and subtrees 4 and 5 are below two black nodes (G and U before, P and U after). Subtrees 1, 2 and 3 each have one more black node than subtrees 4 and 5.

Answer 2

I just read it deeply, and it seems there was a problem with the picture.

Since N is the node which just been insert it means that before the last insert under P there were the children [1,3] or [2,3] (and the insert was of 2 or 1 respectfully). So in that case before the last insert P and U must have been red (and 4,5 are black).