Problem with Precision floating point operation in C

Question

For one of my course project I started implementing "Naive Bayesian classifier" in C. My project is to implement a document classifier application (especially Spam) using huge training data.

Now I have problem implementing the algorithm because of the limitations in the C's datatype.

( Algorithm I am using is given here, http://en.wikipedia.org/wiki/Bayesian_spam_filtering )

PROBLEM STATEMENT: The algorithm involves taking each word in a document and calculating probability of it being spam word. If p1, p2 p3 .... pn are probabilities of word-1, 2, 3 ... n. The probability of doc being spam or not is calculated using

Here, probability value can be very easily around 0.01. So even if I use datatype "double" my calculation will go for a toss. To confirm this I wrote a sample code given below.

#define PROBABILITY_OF_UNLIKELY_SPAM_WORD     (0.01)
#define PROBABILITY_OF_MOSTLY_SPAM_WORD     (0.99)

int main()
{
    int index;
    long double numerator = 1.0;
    long double denom1 = 1.0, denom2 = 1.0;
    long double doc_spam_prob;

    /* Simulating FEW unlikely spam words  */
    for(index = 0; index < 162; index++)
    {
        numerator = numerator*(long double)PROBABILITY_OF_UNLIKELY_SPAM_WORD;
        denom2    = denom2*(long double)PROBABILITY_OF_UNLIKELY_SPAM_WORD;
        denom1    = denom1*(long double)(1 - PROBABILITY_OF_UNLIKELY_SPAM_WORD);
    }
    /* Simulating lot of mostly definite spam words  */
    for (index = 0; index < 1000; index++)
    {
        numerator = numerator*(long double)PROBABILITY_OF_MOSTLY_SPAM_WORD;
        denom2    = denom2*(long double)PROBABILITY_OF_MOSTLY_SPAM_WORD;
        denom1    = denom1*(long double)(1- PROBABILITY_OF_MOSTLY_SPAM_WORD);
    }
    doc_spam_prob= (numerator/(denom1+denom2));
    return 0;
}

I tried Float, double and even long double datatypes but still same problem.

Hence, say in a 100K words document I am analyzing, if just 162 words are having 1% spam probability and remaining 99838 are conspicuously spam words, then still my app will say it as Not Spam doc because of Precision error (as numerator easily goes to ZERO)!!!.

This is the first time I am hitting such issue. So how exactly should this problem be tackled?

Answer 1

This happens often in machine learning. AFAIK, there's nothing you can do about the loss in precision. So to bypass this, we use the log function and convert divisions and multiplications to subtractions and additions, resp.

SO I decided to do the math,

The original equation is:

I slightly modify it:

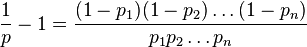
Taking logs on both sides:

Let,

Substituting,

Hence the alternate formula for computing the combined probability:

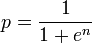
If you need me to expand on this, please leave a comment.

Answer 2

Here's a trick:

for the sake of readability, let S := p_1 * ... * p_n and H := (1-p_1) * ... * (1-p_n), 
then we have:

  p = S / (S + H)
  p = 1 / ((S + H) / S)
  p = 1 / (1 + H / S)

let`s expand again:

  p = 1 / (1 +  ((1-p_1) * ... * (1-p_n)) / (p_1 * ... * p_n))
  p = 1 / (1 + (1-p_1)/p_1 * ... * (1-p_n)/p_n)

So basically, you will obtain a product of quite large numbers (between 0 and, for p_i = 0.01, 99). The idea is, not to multiply tons of small numbers with one another, to obtain, well, 0, but to make a quotient of two small numbers. For example, if n = 1000000 and p_i = 0.5 for all i, the above method will give you 0/(0+0) which is NaN, whereas the proposed method will give you 1/(1+1*...1), which is 0.5.

You can get even better results, when all p_i are sorted and you pair them up in opposed order (let's assume p_1 < ... < p_n), then the following formula will get even better precision:

  p = 1 / (1 + (1-p_1)/p_n * ... * (1-p_n)/p_1)

that way you devide big numerators (small p_i) with big denominators (big p_(n+1-i)), and small numerators with small denominators.

edit: MSalter proposed a useful further optimization in his answer. Using it, the formula reads as follows:

  p = 1 / (1 + (1-p_1)/p_n * (1-p_2)/p_(n-1) * ... * (1-p_(n-1))/p_2 * (1-p_n)/p_1)

Answer 3

Your problem is caused because you are collecting too many terms without regard for their size. One solution is to take logarithms. Another is to sort your individual terms. First, let's rewrite the equation as 1/p = 1 + ∏((1-p_i)/p_i). Now your problem is that some of the terms are small, while others are big. If you have too many small terms in a row, you'll underflow, and with too many big terms you'll overflow the intermediate result.

So, don't put too many of the same order in a row. Sort the terms (1-p_i)/p_i. As a result, the first will be the smallest term, the last the biggest. Now, if you'd multiply them straight away you would still have an underflow. But the order of calculation doesn't matter. Use two iterators into your temporary collection. One starts at the beginning (i.e. (1-p_0)/p_0), the other at the end (i.e (1-p_n)/p_n), and your intermediate result starts at 1.0. Now, when your intermediate result is >=1.0, you take a term from the front, and when your intemediate result is < 1.0 you take a result from the back.

The result is that as you take terms, the intermediate result will oscillate around 1.0. It will only go up or down as you run out of small or big terms. But that's OK. At that point, you've consumed the extremes on both ends, so it the intermediate result will slowly approach the final result.

There's of course a real possibility of overflow. If the input is completely unlikely to be spam (p=1E-1000) then 1/p will overflow, because ∏((1-p_i)/p_i) overflows. But since the terms are sorted, we know that the intermediate result will overflow only if ∏((1-p_i)/p_i) overflows. So, if the intermediate result overflows, there's no subsequent loss of precision.

Answer 4

Try computing the inverse 1/p. That gives you an equation of the form 1 + 1/(1-p1)*(1-p2)...

If you then count the occurrence of each probability--it looks like you have a small number of values that recur--you can use the pow() function--pow(1-p, occurences_of_p)*pow(1-q, occurrences_of_q)--and avoid individual roundoff with each multiplication.

Answer 5

You can use probability in percents or promiles:

doc_spam_prob= (numerator*100/(denom1+denom2));

or

doc_spam_prob= (numerator*1000/(denom1+denom2));

or use some other coefficient