Inorder tree traversal: Which definition is correct?

Question

I have the following text from an academic course I took a while ago about inorder traversal (they also call it pancaking) of a binary tree (not BST):

Inorder tree traversal

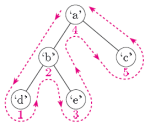
Draw a line around the outside of the tree. Start to the left of the root, and go around the outside of the tree, to end up to the right of the root. Stay as close to the tree as possible, but do not cross the tree. (Think of the tree — its branches and nodes — as a solid barrier.) The order of the nodes is the order in which this line passes underneath them. If you are unsure as to when you go “underneath” a node, remember that a node “to the left” always comes first.

Here's the example used (slightly different tree from below)

However when I do a search on google, I get a conflicting definition. For example the wikipedia example:

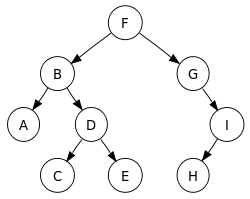
Inorder traversal sequence: A, B, C, D, E, F, G, H, I (leftchild,rootnode,right node)

But according to (my understanding of) definition #1, this should be

A, B, D, C, E, F, G, I, H

Can anyone clarify which definition is correct? They might be both describing different traversal methods, but happen to be using the same name. I'm having trouble believing the peer-reviewed academic text is wrong, but can't be certain.

Answer 1

In my bad attempt at the drawing here's the order that shows how they should be picked.

pretty much pick the node that is directly above the line being drawn,.