In "aa67bc54c9", is there any way to print "aa" 67 times, "bc" 54 times and so on, using regular expressions?

Question

I was asked this question in an interview for an internship, and the first solution I suggested was to try and use a regular expression (I usually am a little stumped in interviews). Something like this

(?P<str>[a-zA-Z]+)(?P<n>[0-9]+)

I thought it would match the strings and store them in the variable "str" and the numbers in the variable "n". How, I was not sure of.

So it matches strings of type "a1b2c3", but a problem here is that it also matches strings of type "a1b". Could anyone suggest a solution to deal with this problem?

Also, is there any other regular expression that could solve this problem?

Answer 1

Do you know why "regular expressions" are called "regular"? :-)

That would be too long to explain, I'll just outline the way. To match a pattern (i.e. decide whether a given string is "valid" or "invalid"), a theoretical informatician would use a finite state automaton. That's an abstract machine that has a finite number of states; each tick it reads a char from the input and jumps to another state. The pattern of where to jump from particular state when a particular character is read is fixed. Some states are marked as "OK", some--as "FAIL", so that by examining state of a machine you can check whether your text is "valid" (i.e. a valid e-mail).

For example, this machine only accepts "nice" as its "valid" word (a pic from Wikipedia):

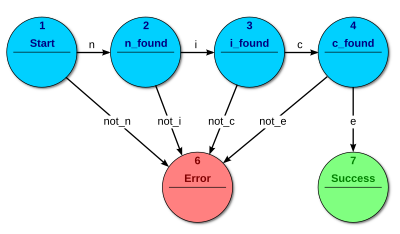
A set of "valid" words such a machine theoretically can distinguish from invalid is called "regular language". Not every set is a regular language: for example, finite state automata are incapable of checking whether parentheses in string are balanced.

But constructing state machines was a complex task, compared to the complexity of defining what "valid" is. So the mathematicians (mainly S. Kleene) noted that every regular language could be described with a "regular expression". They had *s and |s and were the prototypes of what we know as regexps now.

---

What does it have to do with the problem? The problem in subject is essentially non-regular. It can't be expressed with anything that works like a finite automaton.

The essence is that it should contain a memory cell that is capable to hold an arbitrary number (repetition count in your case). Finite automata and classical regular expressions can not do this.

However, modern regexps are more expressive and are said to be able to check balanced parentheses! But this may serve as a good example that you shouldn't use regexps for tasks they don't suit. Let alone that it contains code snippets; this makes the expression far from being "regular".

Answering the initial question, you can't solve your problem with using anything "regular" only. However, regexps could be aid you in solving this problem, as in tster's answer

---

Perhaps, I should look closer to tster's answer (do a "+1" there, please!) and show why it's not the "regular expression" solution. One may think that it is, it just contains print statement (not essential) and a loop--and loop concept is compatible with finite state automaton expressive power. But there is one more elusive thing:

while ($line =~ s/^([a-z]+)(\d+)//i)
{
    print $1 
             x  # <--- this one
               $2;
}

The task of reading a string and a number and printing repeatedly that string given number of times, where the number is an arbitrary integer, is undoable on a finite state machine without additional memory. You use a memory cell to keep that number and decrease it, and check for it to be greater than zero. But this number may be arbitrarily big, and it contradicts with a finite memory available to the finite state machine.

However, there's nothing wrong with classical pattern /([abc]*){5}/ that matches something "regular" repeated fixed number of times. We essentially have states that correspond to "matched pattern once", "matched pattern twice" ... "matched pattern 5 times". There's finite number of them, and that's the gist of the difference.

Answer 2

how about:

while ($line =~ s/^([a-z]+)(\d+)//i)
{
    print $1 x $2;
}