Ideal algorithm for finding all paths in a graph [duplicate]

Question

Let's take this graph for example:

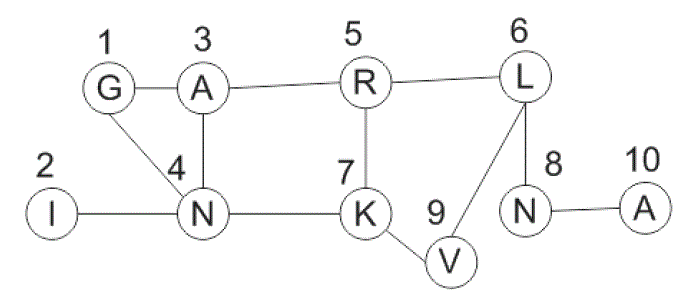
Now let's say I'm starting at vertex 3 and want to find vertex 7. Depth first search (depending on the implementation) will look at the children first. Now, in our example, for the sake of the argument, I start at vertex 2, then go to vertex 4 and vertex 2, returns to vertex and goes to vertex 7, problem solved.

What I'd like: I'd like to get all the possible paths that would get me from x to y (e.g. 3 to 7: 3,1,4,7 - 3,5,7 - 3,4,7 - 3,5,6,9,7). That I don't get from Depth first search.

What is the algorithm you'd suggest?

Thank you!

Answer 1

You should use modified BFS algorithm (http://en.wikipedia.org/wiki/Breadth-first_search). On each vertex you should save list of neighbors, which are leading to this vertex(predecessors) instead of having just 1 neighbor leading to this vertex.

When you want to find all paths from this you just have to start on your end node and branch your path at every vertex, that have more than 1 predecessor and go with the way created by predecessors in each vertex until you get to start node with all branches you have.

EDIT: You can use DSF algorithm instead of BFS and modify it in a same way.