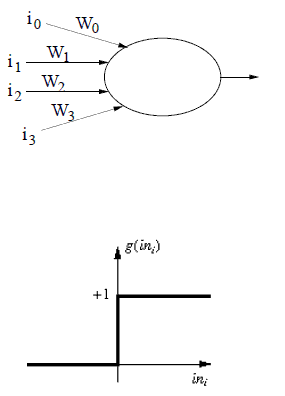
I'm trying to determine for the articial neuron shown below the values (0 or 1) for the inputs i1, i2, and i3 for which it will fire (i0 is the input for the bias weight and will always be -1).
The weights are
W0 = 1.5
W1 = -1
W2 = 1, and W3 = 2.
Assume the activation function depicted in image below.
Please clarify your answer as I have done few examples and still I'm not able to fully understand the theory :(
Many thanks,
Mary J.
PS. Image below:
$w_1$ is the weight of connection between 1 and 3. $w_2$ is the weight of connection between 2 and 3. So the input to neuron 3 is $i =o_1w_1 +o_2w_2$ Let the activation function of neuron 3 be sigmoid function. $f(x) = \dfrac{1}{1+e^{-x}}$ and the threshold value of neuron 3 be $\theta$.
These certain conditions which differ neuron to neuron are called Threshold. For example, if the input X1 into the first neuron is 30 and X2 is 0: This neuron will not fire, since the sum 30+0 = 30 is not greater than the threshold i.e 100.
Neural networks can usually be read from left to right. Here, the first layer is the layer in which inputs are entered. There are 2 internals layers (called hidden layers) that do some math, and one last layer that contains all the possible outputs. Don't bother with the “+1”s at the bottom of every columns.
An artificial neuron simulates how a biological neuron behaves by adding together the values of the inputs it receives. If this is above some threshold, it sends its own signal to its output, which is then received by other neurons. However, a neuron doesn't have to treat each of its inputs with equal weight.
You basically have the following equation for the neuron output, where i1, i2, and i3 can each have the value 0 or 1:
2*i3 + i2 - i1 - 1.5 >= 0
First, let's look at the highest positively-weighted value. If i3 is 0, the most you can get for the left side is -0.5, so i3 has to be 1 to get a non-zero output. The equation then becomes:
i2 - i1 + 0.5 >= 0
Now look at the negatively-weighted value. If i1 is 0, the output will always be greater than zero no matter what i2 is. If i1 is 1, i2 has to be 1 as well for there to be a non-zero output.
You therefore have these combinations which create a non-zero output:
i1 i2 i3
0 0 1
0 1 1
1 1 1
If you love us? You can donate to us via Paypal or buy me a coffee so we can maintain and grow! Thank you!
Donate Us With