How to avoid impression bias when calculate the ctr?

Question

When we train a ctr(click through rate) model, sometimes we need calcute the real ctr from the history data, like this

                 #(click)
    ctr   =  ----------------
              #(impressions)

We know that, if the number of impressions is too small, the calculted ctr is not real. So we always set a threshold to filter out the large enough impressions.

But we know that the higher impressions, the higher confidence for the ctr. Then my question is that: Is there a impressions-normalized statistic method to calculate the ctr?

Thanks!

Answer 1

You probably need a representation of confidence interval for your estimated ctr. Wilson score interval is a good one to try.

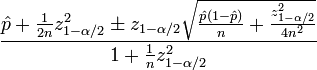
You need below stats to calculate the confidence score:

• \hat p is the observed ctr (fraction of #clicked vs #impressions)
• n is the total number of impressions
• z_α/2 is the (1-α/2) quantile of the standard normal distribution

A simple implementation in python is shown below, I use z_(1-α/2)=1.96 which corresponds to a 95% confidence interval. I attached 3 test results at the end of the code.

# clicks      # impressions       # conf interval
2             10                  (0.07, 0.45)
20            100                 (0.14, 0.27)
200           1000                (0.18, 0.22)

Now you can set up some threshold to use the calculated confidence interval.

from math import sqrt

def confidence(clicks, impressions):
    n = impressions
    if n == 0: return 0
    z = 1.96 #1.96 -> 95% confidence
    phat = float(clicks) / n
    denorm = 1. + (z*z/n)
    enum1 = phat + z*z/(2*n)
    enum2 = z * sqrt(phat*(1-phat)/n + z*z/(4*n*n))
    return (enum1-enum2)/denorm, (enum1+enum2)/denorm

def wilson(clicks, impressions):
    if impressions == 0:
        return 0
    else:
        return confidence(clicks, impressions)

if __name__ == '__main__':
    print wilson(2,10)
    print wilson(20,100)
    print wilson(200,1000)

"""    
--------------------
results:
(0.07048879557839793, 0.4518041980521754)
(0.14384999046998084, 0.27112660859398174)
(0.1805388068716823, 0.22099327100894336)
"""

Answer 2

If you treat this as a binomial parameter, you can do Bayesian estimation. If your prior on ctr is uniform (a Beta distribution with parameters (1,1)) then your posterior is Beta(1+#click, 1+#impressions-#click). Your posterior mean is #click+1 / #impressions+2 if you want a single summary statistic of this posterior, but you probably don't, and here's why:

I don't know what your method for determining whether ctr is high enough, but let's say you're interested in everything with ctr > 0.9. You can then use the cumulative density function of the beta distribution to look at what proportion of probability mass is over the 0.9 threshold (this will just be 1 - the cdf at 0.9). In this way, your threshold will naturally incorporate uncertainty about the estimate because of limited sample size.