How do I construct the biadjacency matrix of a DAG?

Question

For a bipartite graph, you can substitute the adjacency matrix with what is called its biadjacency matrix:

The adjacency matrix A of a bipartite graph whose parts have r and s vertices has the form

    A =  O  B
         BT O

where B is an r × s matrix and O is an all-zero matrix. Clearly, the matrix B uniquely represents the bipartite graphs, and it is commonly called its biadjacency matrix.

Now, a DAG is a bipartite graph, for example, you could topologically sort it and have the sets U and V being nodes that are on an odd or even topological level, respectively.

This means, that for a DAG with n nodes, I only need a (n/2)² matrix (on average) instead of a n² matrix. Problem is, I don't know how to construct it. Any hints?

Answer 1

I believe you can't construct a biadjacency matrix for a DAG, because not every DAG is a bipartite graph.

Here is a simple example: consider a directed graph with 3 vertices, and denote them as A, B and C. The edges connect A to B, B to C and A to C. The graph is clearly a DAG, since it is directed and there are no cycles (A->B->C<-A isn't a cycle). However, the graph is not bipartite: there is no way to divide A, B and C to two disjoint sets, where there are no edges between vertices in the same set.

The conclusion is that there graphes which are DAGs but not bipartite, so not every DAG is bipartite.

Note that the fact that you can topologically sort a DAG and divide the vertices to two disjoint sets, does not mean there are no edges between vertices of the same set.

Answer 2

It seems that the biadjacency matrix B for the A matrix can only be constructed when the graph is undirected.

Based on the example from Wikipedia:

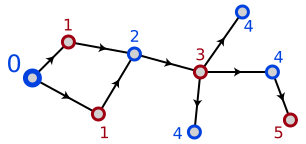
The adjacency matrices for this DAG should be:

Blue -> Red
B = 1 1 0 0
    0 0 1 0
    0 0 0 0
    0 0 0 0
    0 0 0 1

Red -> Blue
C = 0 1 0 0 0
    0 1 0 0 0
    0 0 1 1 1
    0 0 0 0 0

As you can see C is not the transpose of B. It doesn't appear possible to create an A matrix as described. However, you could create an A matrix like this:

A = 0 B
    C 0

This would require 2 * (n/2)^2 space which is still better than n^2.

To construct the B and C matrices you just need to loop over each node in U and V (respectively) to determine the outbound edges.