Expressing an integer as a series of multipliers

Question

Scroll down to see latest edit, I left all this text here just so that I don't invalidate the replies this question has received so far!

---

I have the following brain teaser I'd like to get a solution for, I have tried to solve this but since I'm not mathematically that much above average (that is, I think I'm very close to average) I can't seem wrap my head around this.

The problem: Given number x should be split to a serie of multipliers, where each multiplier <= y, y being a constant like 10 or 16 or whatever. In the serie (technically an array of integers) the last number should be added instead of multiplied to be able to convert the multipliers back to original number.

As an example, lets assume x=29 and y=10. In this case the expected array would be {10,2,9} meaning 10*2+9. However if y=5, it'd be {5,5,4} meaning 5*5+4 or if y=3, it'd be {3,3,3,2} which would then be 3*3*3+2.

I tried to solve this by doing something like this:

1. while x >= y, store y to multipliers, then x = x - y
2. when x < y, store x to multipliers

Obviously this didn't work, I also tried to store the "leftover" part separately and add that after everything else but that didn't work either. I believe my main problem is that I try to think this in a way too complex manner while the solution is blatantly obvious and simple.

To reiterate, these are the limits this algorithm should have:

• has to work with 64bit longs
• has to return an array of 32bit integers (...well, shorts are OK too)
• while support for signed numbers (both + and -) would be nice, if it helps the task only unsigned numbers is a must

And while I'm doing this using Java, I'd rather take any possible code examples as pseudocode, I specifically do NOT want readily made answers, I just need a nudge (well, more of a strong kick) so that I can solve this at least partly myself. Thanks in advance.

Edit: Further clarification

To avoid some confusion, I think I should reword this a bit:

• Every integer in the result array should be less or equal to y, including the last number.
• Yes, the last number is just a magic number.
• No, this is isn't modulus since then the second number would be larger than y in most cases.
• Yes, there is multiple answers to most of the numbers available, however I'm looking for the one with least amount of math ops. As far as my logic goes, that means finding the maximum amount of as big multipliers as possible, for example x=1 000 000,y=100 is 100*100*100 even though 10*10*10*10*10*10 is equally correct answer math-wise.

I need to go through the given answers so far with some thought but if you have anything to add, please do! I do appreciate the interest you've already shown on this, thank you all for that.

Edit 2: More explanations + bounty

Okay, seems like what I was aiming for in here just can't be done the way I thought it could be. I was too ambiguous with my goal and after giving it a bit of a thought I decided to just tell you in its entirety what I'd want to do and see what you can come up with.

My goal originally was to come up with a specific method to pack 1..n large integers (aka longs) together so that their String representation is notably shorter than writing the actual number. Think multiples of ten, 10^6 and 1 000 000 are the same, however the representation's length in characters isn't.

For this I wanted to somehow combine the numbers since it is expected that the numbers are somewhat close to each other. I firsth thought that representing 100, 121, 282 as 100+21+161 could be the way to go but the saving in string length is neglible at best and really doesn't work that well if the numbers aren't very close to each other. Basically I wanted more than ~10%.

So I came up with the idea that what if I'd group the numbers by common property such as a multiplier and divide the rest of the number to individual components which I can then represent as a string. This is where this problem steps in, I thought that for example 1 000 000 and 100 000 can be expressed as 10^(5|6) but due to the context of my aimed usage this was a bit too flaky:

The context is Web. RESTful URL:s to be specific. That's why I mentioned of thinking of using 64 characters (web-safe alphanumberic non-reserved characters and then some) since then I could create seemingly random URLs which could be unpacked to a list of integers expressing a set of id numbers. At this point I thought of creating a base 64-like number system for expressing base 10/2 numbers but since I'm not a math genius I have no idea beyond this point how to do it.

The bounty

Now that I have written the whole story (sorry that it's a long one), I'm opening a bounty to this question. Everything regarding requirements for the preferred algorithm specified earlier is still valid. I also want to say that I'm already grateful for all the answers I've received so far, I enjoy being proven wrong if it's done in such a manner as you people have done.

The conclusion

Well, bounty is now given. I spread a few comments to responses mostly for future reference and myself, you can also check out my SO Uservoice suggestion about spreading bounty which is related to this question if you think we should be able to spread it among multiple answers.

---

Thank you all for taking time and answering!

Answer 1

Update

I couldn't resist trying to come up with my own solution for the first question even though it doesn't do compression. Here is a Python solution using a third party factorization algorithm called pyecm.

This solution is probably several magnitudes more efficient than Yevgeny's one. Computations take seconds instead of hours or maybe even weeks/years for reasonable values of y. For x = 2^32-1 and y = 256, it took 1.68 seconds on my core duo 1.2 ghz.

>>> import time
>>> def test():
...     before = time.time()
...     print factor(2**32-1, 256)
...     print time.time()-before
...
>>> test()
[254, 232, 215, 113, 3, 15]
1.68499994278
>>> 254*232*215*113*3+15
4294967295L

And here is the code:

def factor(x, y):
    # y should be smaller than x. If x=y then {y, 1, 0} is the best solution
    assert(x > y)

    best_output = []

    # try all possible remainders from 0 to y 
    for remainder in xrange(y+1):
        output = []
        composite = x - remainder
        factors = getFactors(composite)

        # check if any factor is larger than y
        bad_remainder = False
        for n in factors.iterkeys():
            if n > y: 
                bad_remainder = True
                break
        if bad_remainder: continue

        # make the best factors
        while True:
            results = largestFactors(factors, y)
            if results == None: break
            output += [results[0]]
            factors = results[1]

        # store the best output
        output = output + [remainder]
        if len(best_output) == 0 or len(output) < len(best_output):
            best_output = output

    return best_output

# Heuristic
# The bigger the number the better. 8 is more compact than 2,2,2 etc...

# Find the most factors you can have below or equal to y
# output the number and unused factors that can be reinserted in this function
def largestFactors(factors, y):
    assert(y > 1)
    # iterate from y to 2 and see if the factors are present.
    for i in xrange(y, 1, -1):
        try_another_number = False
        factors_below_y = getFactors(i)
        for number, copies in factors_below_y.iteritems():
            if number in factors:
                if factors[number] < copies:
                    try_another_number = True
                    continue # not enough factors
            else:
                try_another_number = True
                continue # a factor is not present

        # Do we want to try another number, or was a solution found?
        if try_another_number == True:
            continue
        else:
            output = 1
            for number, copies in factors_below_y.items():
                remaining = factors[number] - copies
                if remaining > 0:
                    factors[number] = remaining
                else:
                    del factors[number]
                output *= number ** copies

            return (output, factors)

    return None # failed




# Find prime factors. You can use any formula you want for this.
# I am using elliptic curve factorization from http://sourceforge.net/projects/pyecm
import pyecm, collections, copy

getFactors_cache = {}
def getFactors(n):
    assert(n != 0)
    # attempt to retrieve from cache. Returns a copy
    try:
        return copy.copy(getFactors_cache[n])
    except KeyError:
        pass

    output = collections.defaultdict(int)
    for factor in pyecm.factors(n, False, True, 10, 1):
        output[factor] += 1

    # cache result
    getFactors_cache[n] = output

    return copy.copy(output)

Answer to first question

You say you want compression of numbers, but from your examples, those sequences are longer than the undecomposed numbers. It is not possible to compress these numbers without more details to the system you left out (probability of sequences/is there a programmable client?). Could you elaborate more?

Here is a mathematical explanation as to why current answers to the first part of your problem will never solve your second problem. It has nothing to do with the knapsack problem.

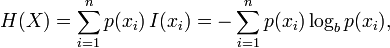
This is Shannon's entropy algorithm. It tells you the theoretical minimum amount of bits you need to represent a sequence {X0, X1, X2, ..., Xn-1, Xn} where p(Xi) is the probability of seeing token Xi.

Let's say that X0 to Xn is the span of 0 to 4294967295 (the range of an integer). From what you have described, each number is as likely as another to appear. Therefore the probability of each element is 1/4294967296.

When we plug it into Shannon's algorithm, it will tell us what the minimum number of bits are required to represent the stream.

import math

def entropy():
    num = 2**32
    probability = 1./num
    return -(num) * probability * math.log(probability, 2)
    # the (num) * probability cancels out

The entropy unsurprisingly is 32. We require 32 bits to represent an integer where each number is equally likely. The only way to reduce this number, is to increase the probability of some numbers, and decrease the probability of others. You should explain the stream in more detail.

Answer to second question

The right way to do this is to use base64, when communicating with HTTP. Apparently Java does not have this in the standard library, but I found a link to a free implementation:

http://iharder.sourceforge.net/current/java/base64/

Here is the "pseudo-code" which works perfectly in Python and should not be difficult to convert to Java (my Java is rusty):

def longTo64(num):
    mapping = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789-_"
    output = ""

    # special case for 0
    if num == 0:
        return mapping[0]

    while num != 0:
        output = mapping[num % 64] + output
        num /= 64

    return output

If you have control over your web server and web client, and can parse the entire HTTP requests without problem, you can upgrade to base85. According to wikipedia, url encoding allows for up to 85 characters. Otherwise, you may need to remove a few characters from the mapping.

Here is another code example in Python

def longTo85(num):
    mapping = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789-_.~!*'();:@&=+$,/?%#[]"
    output = ""
    base = len(mapping)

    # special case for 0
    if num == 0:
        return mapping[0]

    while num != 0:
        output = mapping[num % base] + output
        num /= base

    return output

And here is the inverse operation:

def stringToLong(string):
    mapping = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789-_.~!*'();:@&=+$,/?%#[]"
    output = 0
    base = len(mapping)

    place = 0
    # check each digit from the lowest place
    for digit in reversed(string):
        # find the number the mapping of symbol to number, then multiply by base^place
        output += mapping.find(digit) * (base ** place)
        place += 1

    return output

Here is a graph of Shannon's algorithm in different bases.

As you can see, the higher the radix, the less symbols are needed to represent a number. At base64, ~11 symbols are required to represent a long. At base85, it becomes ~10 symbols.

Answer 2

Edit after final explanation:

I would think base64 is the best solution, since there are standard functions that deal with it, and variants of this idea don't give much improvement. This was answered with much more detail by others here.

Regarding the original question, although the code works, it is not guaranteed to run in any reasonable time, as was answered as well as commented on this question by LFSR Consulting.

Original Answer:

You mean something like this?

Edit - corrected after a comment.

shortest_output = {}

foreach (int R = 0; R <= X; R++) {
    // iteration over possible remainders
    // check if the rest of X can be decomposed into multipliers
    newX = X - R;
    output = {};

    while (newX > Y) {
       int i;
       for (i = Y; i > 1; i--) {
           if ( newX  % i == 0) { // found a divider
           output.append(i);
           newX  = newX /i;  
           break;
           }
       }

       if (i == 1) { // no dividers <= Y
          break;
       }
    }
    if (newX != 1) {
        // couldn't find dividers with no remainder
        output.clear();
    }
    else {
        output.append(R);
            if (output.length() < shortest_output.length()) {
                 shortest_output = output;
            }
    }
}

Answer 3

It sounds as though you want to compress random data -- this is impossible for information theoretic reasons. (See http://www.faqs.org/faqs/compression-faq/part1/preamble.html question 9.) Use Base64 on the concatenated binary representations of your numbers and be done with it.

Answer 4

The problem you're attempting to solve (you're dealing with a subset of the problem, given you're restriction of y) is called Integer Factorization and it cannot be done efficiently given any known algorithm:

In number theory, integer factorization is the breaking down of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer.

This problem is what makes a number of cryptographic functions possible (namely RSA which uses 128 bit keys - long is half of that.) The wiki page contains some good resources that should move you in the right direction with your problem.

So, your brain teaser is indeed a brain teaser... and if you solve it efficiently we can elevate your math skills to above average!