Drawing a Rotated Rectangle

Question

I realize this might be more of a math problem.

To draw the lines for my rectangles I need to solve for their corners. I have a rectangle center at (x,y) With a defined Width and Height.

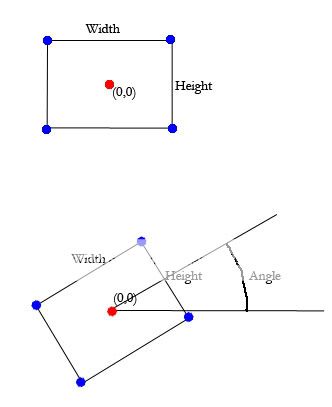
To find the blue points on a non rotated rectangle on top (angle = 0) It is

UL = (x-Width/2),(y+height/2)
UR = (x+Width/2),(y+height/2)
LR = (x+Width/2),(y-height/2)
LL = (x-Width/2),(y-height/2)

How do I find the points if the angle isn't 0?

Thanks in advance.

---

Update: although I have (0,0) in my picture as the center point most likely the center point won't be at that location.

Answer 1

First transform the centre point to 0,0

X' = X-x

Y' = Y-y

Then rotate for an angle of A

X'' = (X-x) * cos A - (Y-y) * sin A

Y'' = (Y-y) * cos A + (X-x) * sin A

Again transform back the centre point to x,y

X''' = (X-x) * cos A - (Y-y) * sin A + x

Y''' = (Y-y) * cos A + (X-x) * sin A + y

Hence compute for all 4 points of (X,Y) with following transformation

X''' = (X-x) * cos A - (Y-y) * sin A + x

Y''' = (Y-y) * cos A + (X-x) * sin A + y

where x, y are the centre points of rectangle and X,Y are the corner points You have n't defined correctly even the corner points when Angle is 0 as I have given in the comments.

After substituting you will get

UL  =  x + ( Width / 2 ) * cos A - ( Height / 2 ) * sin A ,  y + ( Height / 2 ) * cos A  + ( Width / 2 ) * sin A
UR  =  x - ( Width / 2 ) * cos A - ( Height / 2 ) * sin A ,  y + ( Height / 2 ) * cos A  - ( Width / 2 ) * sin A
BL =   x + ( Width / 2 ) * cos A + ( Height / 2 ) * sin A ,  y - ( Height / 2 ) * cos A  + ( Width / 2 ) * sin A
BR  =  x - ( Width / 2 ) * cos A + ( Height / 2 ) * sin A ,  y - ( Height / 2 ) * cos A  - ( Width / 2 ) * sin A

I think this suits your solution.

Answer 2

If 'theta' is the anti-clockwise angle of rotation, then the rotation matrix is:

| cos(theta)  -sin(theta) |
| sin(theta)   cos(theta) |

i.e.

x' = x.cos(theta) - y.sin(theta)
y' = x.sin(theta) + y.cos(theta)

If the rotation point isn't at the origin, subtract the center of rotation from your original coordinates, perform the rotation as shown above, and then add the center of rotation back in again.

There's examples of other transformations at http://en.wikipedia.org/wiki/Transformation_matrix

Answer 3

Rotation matrix (this is becoming a FAQ)

Answer 4

See 2D Rotation.

q = initial angle, f = angle of rotation.

x = r cos q 
y = r sin q

x' = r cos ( q + f ) = r cos q cos f - r sin q sin f 
y' = r sin ( q + w ) = r sin q cos f + r cos q sin f

hence:
x' = x cos f - y sin f
y' = y cos f + x sin f

Answer 5

One of the easiest ways to do this is to take the location of the point before rotation and then apply a coordinate transform. Since it's centred on (0,0), this is simply a case of using:

x' = x cos(theta) - y sin(theta)

y' = y cos(theta) + x sin(theta)