Defining the material conditional in Prolog

Question

I have been trying to acclimate to Prolog and Horn clauses, but the transition from formal logic still feels awkward and forced. I understand there are advantages to having everything in a standard form, but:

What is the best way to define the material conditional operator --> in Prolog, where A --> B succeeds when either A = true and B = true OR B = false? That is, an if->then statement that doesn't fail when if is false without an else.

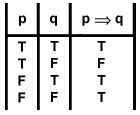
Also, what exactly are the non-obvious advantages of Horn clauses?

Answer 1

What is the best way to define the material conditional operator --> in Prolog

When A and B are just variables to be bound to the atoms true and false, this is easy:

cond(false, _).
cond(_, true).

But in general, there is no best way because Prolog doesn't offer proper negation, only negation as failure, which is non-monotonic. The closest you can come with actual propositions A and B is often

(\+ A ; B)

which tries to prove A, then goes on to B if A cannot be proven (which does not mean that it is false due to the closed-world assumption).

Negation, however, should be used with care in Prolog.

Also, what exactly are the non-obvious advantages of Horn clauses?

That they have a straightforward procedural reading. Prolog is a programming language, not a theorem prover. It's possible to write programs that have a clear logical meaning, but they're still programs.

To see the difference, consider the classical problem of sorting. If L is a list of numbers without duplicates, then

sort(L, S) :-
    permutation(L, S),
    sorted(S).
sorted([]).
sorted([_]).
sorted([X,Y|L]) :-
    X < Y,
    sorted([Y|L]).

is a logical specification of what it means for S to contain the elements of L in sorted order. However, it also has a procedural meaning, which is: try all the permutations of L until you have one that it sorted. This procedure, in the worst case, runs through all n! permutations, even though sorting can be done in O(n lg n) time, making it a very poor sorting program.

See also this question.