The problem i have, is that i need to convert from XYZ fixed axis rotations, to Euler rotations about Z, then X', then Z''.
Here are the relevant matrices:
X: 
Y: 
Z: 
Combined, as Rz(psi) Ry(phi) Rx(theta) = Rxyz(theta,phi,psi); they give:
Rxyz: 
And the Rotation matrix for the Specific convention of Euler angles i want; is this:
Euler: 
So my initial plan, was to compare matrix elements, and extract the angles i wanted that way; I came up with this (actual current code at the end):

But this doesn't work under several circumstances. The most obvious being when Cos(theta)Cos(phi) == 1; since then Cos(beta) = 1, and so Sin[beta] = 0. Where Sin(beta) is s2 in the code. This happens only when Cos(theta) and cos(phi) = +/- 1.
So right away I can just rule out the possible situations;
When theta or phi = 0, 180, 360, 540, ..., then Cos(theta), and Cos(phi) are +/- 1;
so I only need to do it differently for these cases;
And i ended up with this code:
public static double[] ZXZtoEuler(double θ, double φ, double ψ){
θ *= Math.PI/180.0;
φ *= Math.PI/180.0;
ψ *= Math.PI/180.0;
double α = -1;
double β = -1;
double γ = -1;
double c2 = Math.cos(θ) * Math.cos(φ);
β = Math.acos(r(c2));
if(eq(c2,1) || eq(c2,-1)){
if(eq(Math.cos(θ),1)){
if(eq(Math.cos(φ),1)){
α = 0.0;
γ = ψ;
}else if(eq(Math.cos(φ),-1)){
α = 0.0;
γ = Math.PI - ψ;
}
}else if(eq(Math.cos(θ),-1)){
if(eq(Math.cos(φ),1)){
α = 0.0;
γ = -ψ;
}else if(eq(Math.cos(φ),-1)){
α = 0.0;
γ = ψ + Math.PI;
}
}
}else{
//original way
double s2 = Math.sin(β);
double c3 = ( Math.sin(θ) * Math.cos(φ) )/ s2;
double s1 = ( Math.sin(θ) * Math.sin(ψ) + Math.cos(θ) * Math.sin(φ) * Math.cos(ψ) )/s2;
γ = Math.acos(r(c3));
α = Math.asin(r(s1));
}
α *= 180/Math.PI;
β *= 180/Math.PI;
γ *= 180/Math.PI;
return new double[] {r(α), r(β), r(γ)};
}
Where r and eq are just two simple functions;
public static double r(double a){
double prec = 1000000000.0;
return Math.round(a*prec)/prec;
}
static double thresh = 1E-4;
public static boolean eq(double a, double b){
return (Math.abs(a-b) < thresh);
}
eq is just to compare the numbers for tests, and r is to prevent floating point errors pushing numbers outside the range of Math.acos / Math.asin and giving me NaN results;
(i.e. every now and then i'd end up with Math.acos(1.000000000000000004) or something.)
Which takes into account the 4 cases of having rotations around x and y which leave c2==1.
But now is where the problem occurs;
Everything I have done above, makes sense to me, but it does not give the correct angles;
Here is some output, in each pair, the first are the theta phi psi angles, and the second of each pair is the corresponding alpha beta gamma lines. Ignoring the rounding errors, it seems to be getting some of the angles off by about
[0.0, 0.0, 0.0] - correct!
[0.0, 0.0, 0.0]
[0.0, 0.0, 45.0] - correct!
[0.0, 0.0, 45.0]
[0.0, 0.0, 90.0] - correct!
[0.0, 0.0, 90.0]
[0.0, 0.0, 135.0] - correct!
[0.0, 0.0, 135.0]
[0.0, 0.0, 180.0] - correct
[0.0, 0.0, 180.0]
[0.0, 0.0, 225.0] - correct
[0.0, 0.0, 225.0]
[0.0, 0.0, 270.0] - correct
[0.0, 0.0, 270.0]
[0.0, 0.0, 315.0] - correct
[0.0, 0.0, 315.0]
[0.0, 45.0, 0.0] - incorrect: should be [90, 45, -90]
[90.0, 44.999982, 90.0]
[0.0, 45.0, 45.0]
[45.000018, 44.999982, 90.0]
[0.0, 45.0, 90.0]
[0.0, 44.999982, 90.0]
[0.0, 45.0, 135.0]
[-45.000018, 44.999982, 90.0]
[0.0, 45.0, 180.0]
[-90.0, 44.999982, 90.0]
[0.0, 45.0, 225.0]
[-45.000018, 44.999982, 90.0]
[0.0, 45.0, 270.0]
[0.0, 44.999982, 90.0]
[0.0, 45.0, 315.0]
[45.000018, 44.999982, 90.0]
[0.0, 90.0, 0.0]
[90.0, 90.0, 90.0]
[0.0, 90.0, 45.0]
[45.000018, 90.0, 90.0]
[0.0, 90.0, 90.0]
[0.0, 90.0, 90.0]
[0.0, 90.0, 135.0]
[-45.000018, 90.0, 90.0]
[0.0, 90.0, 180.0]
[-90.0, 90.0, 90.0]
[0.0, 90.0, 225.0]
[-45.000018, 90.0, 90.0]
i think it's due to the way Math.acos and Math.asin work, Can anyone think of a solution?
EDIT: math.asin and math.acos return values between -pi/2 and pi/2 and 0 and pi respectively. This is not ambiguous, so i don't think the problem is here. It seems like i might have the maths wrong somewhere, but i can't see a hole in my reasoning...
EDIT2: To anyone how doesn't know how Euler rotations work, it's like this:
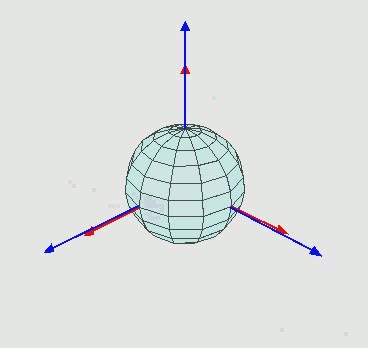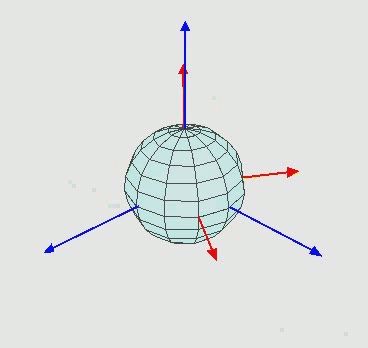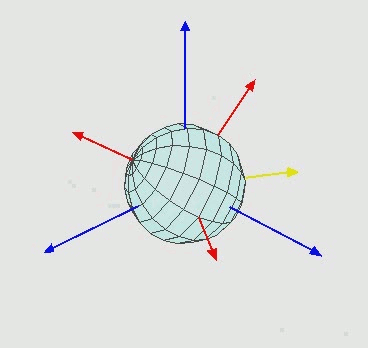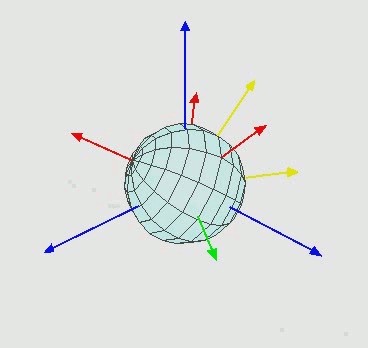
That is, rotate around Z, then around the new X axis (X') then around the new Z'' axis.
rotm = eul2rotm( eul , sequence ) converts Euler angles to a rotation matrix, rotm . The Euler angles are specified in the axis rotation sequence, sequence . The default order for Euler angle rotations is "ZYX" .
Euler angles can be defined by intrinsic rotations. The rotated frame XYZ may be imagined to be initially aligned with xyz, before undergoing the three elemental rotations represented by Euler angles. Its successive orientations may be denoted as follows: x-y-z, or x0-y0-z0 (initial)
The ZYX Euler angles (α,β,γ) refer to the angles of rotation about the three joint axes of the wrist mechanism, and the orientation of the end-effector can be expressed by the matrix R(α,β,γ) found above. The wrist mechanism when β = 90o.
Euler rotation is prone to the problem of Gimbal Lock, where two of the axes overlap and lead to the same result. Quaternion rotation uses a more complex algorithm that helps it avoid Gimbal Lock problems.
I haven't completely figured this out, but one thing I did notice: You use the arccos/arcsin functions as if cos/sin were bijective, just taking their inverse. However, when taking the arccos, consider the general solutions to the arc functions. For example, when cos y = x, then there are two (well, infinitely many) solutions:
y = arccos x + 2kPI, where k element Z
y = 2PI - arccos x + 2kPI, k as aboveWith k=-1, the last equation reduces to
y = -arccos xSo in total, y = +- arccos x. This essentially boils down to the fact that cos is axially symmetric to x=0. An analogous argument applies to arcsin, leading to y = PI - asin x (with k=0 in the general solution of sin y = x)
This immediatelly applies to your code. The statement γ = Math.acos(r(c3)); somehow must take the sign into account. I struggle with this one, there must be a criteria to sort out the "incorrect" solution.
If you love us? You can donate to us via Paypal or buy me a coffee so we can maintain and grow! Thank you!
Donate Us With