Conditionally colour data points outside of confidence bands in R

Question

I need to colour datapoints that are outside of the the confidence bands on the plot below differently from those within the bands. Should I add a separate column to my dataset to record whether the data points are within the confidence bands? Can you provide an example please?

Example dataset:

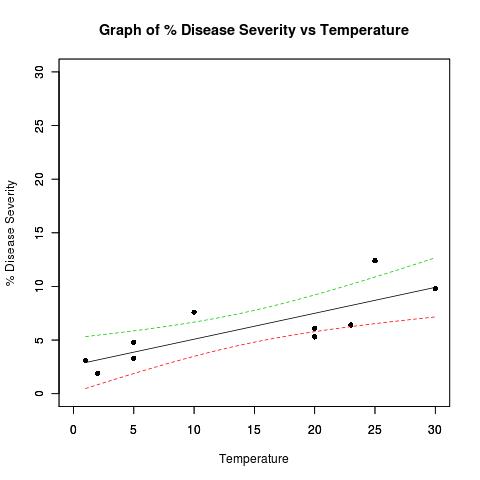
## Dataset from http://www.apsnet.org/education/advancedplantpath/topics/RModules/doc1/04_Linear_regression.html

## Disease severity as a function of temperature

# Response variable, disease severity
diseasesev<-c(1.9,3.1,3.3,4.8,5.3,6.1,6.4,7.6,9.8,12.4)

# Predictor variable, (Centigrade)
temperature<-c(2,1,5,5,20,20,23,10,30,25)

## For convenience, the data may be formatted into a dataframe
severity <- as.data.frame(cbind(diseasesev,temperature))

## Fit a linear model for the data and summarize the output from function lm()
severity.lm <- lm(diseasesev~temperature,data=severity)

# Take a look at the data
plot(
  diseasesev~temperature,
  data=severity,
  xlab="Temperature",
  ylab="% Disease Severity",
  pch=16,
  pty="s",
  xlim=c(0,30),
  ylim=c(0,30)
)
title(main="Graph of % Disease Severity vs Temperature")
par(new=TRUE) # don't start a new plot

## Get datapoints predicted by best fit line and confidence bands
## at every 0.01 interval
xRange=data.frame(temperature=seq(min(temperature),max(temperature),0.01))
pred4plot <- predict(
                        lm(diseasesev~temperature),
                        xRange,
                        level=0.95,
                        interval="confidence"
                    )

## Plot lines derrived from best fit line and confidence band datapoints
matplot(
  xRange,
  pred4plot,
  lty=c(1,2,2),   #vector of line types and widths
  type="l",       #type of plot for each column of y
  xlim=c(0,30),
  ylim=c(0,30),
  xlab="",
  ylab=""
)

Answer 1

Well, I thought that this would be pretty easy with ggplot2, but now I realize that I have no idea how the confidence limits for stat_smooth/geom_smooth are calculated.

Consider the following:

library(ggplot2)
pred <- as.data.frame(predict(severity.lm,level=0.95,interval="confidence"))
dat <- data.frame(diseasesev,temperature, 
    in_interval = diseasesev <=pred$upr & diseasesev >=pred$lwr ,pred)
ggplot(dat,aes(y=diseasesev,x=temperature)) +
stat_smooth(method='lm')  + geom_point(aes(colour=in_interval)) +
    geom_line(aes(y=lwr),colour=I('red')) + geom_line(aes(y=upr),colour=I('red'))

This produces: alt text http://ifellows.ucsd.edu/pmwiki/uploads/Main/strangeplot.jpg

I don't understand why the confidence band calculated by stat_smooth is inconsistent with the band calculated directly from predict (i.e. the red lines). Can anyone shed some light on this?

Edit:

figured it out. ggplot2 uses 1.96 * standard error to draw the intervals for all smoothing methods.

pred <- as.data.frame(predict(severity.lm,se.fit=TRUE,
        level=0.95,interval="confidence"))
dat <- data.frame(diseasesev,temperature, 
    in_interval = diseasesev <=pred$fit.upr & diseasesev >=pred$fit.lwr ,pred)
ggplot(dat,aes(y=diseasesev,x=temperature)) +
    stat_smooth(method='lm')  + 
    geom_point(aes(colour=in_interval)) +
    geom_line(aes(y=fit.lwr),colour=I('red')) + 
    geom_line(aes(y=fit.upr),colour=I('red')) +
    geom_line(aes(y=fit.fit-1.96*se.fit),colour=I('green')) + 
    geom_line(aes(y=fit.fit+1.96*se.fit),colour=I('green'))

Answer 2

The easiest way is probably to calculate a vector of TRUE/FALSE values that indicate if a data point is inside of the confidence interval or not. I'm going to reshuffle your example a little bit so that all of the calculations are completed before the plotting commands are executed- this provides a clean separation in the program logic that could be exploited if you were to package some of this into a function.

The first part is pretty much the same, except I replaced the additional call to lm() inside predict() with the severity.lm variable- there is no need to use additional computing resources to recalculate the linear model when we already have it stored:

## Dataset from 
#  apsnet.org/education/advancedplantpath/topics/
#    RModules/doc1/04_Linear_regression.html

## Disease severity as a function of temperature

# Response variable, disease severity
diseasesev<-c(1.9,3.1,3.3,4.8,5.3,6.1,6.4,7.6,9.8,12.4)

# Predictor variable, (Centigrade)
temperature<-c(2,1,5,5,20,20,23,10,30,25)

## For convenience, the data may be formatted into a dataframe
severity <- as.data.frame(cbind(diseasesev,temperature))

## Fit a linear model for the data and summarize the output from function lm()
severity.lm <- lm(diseasesev~temperature,data=severity)

## Get datapoints predicted by best fit line and confidence bands
## at every 0.01 interval
xRange=data.frame(temperature=seq(min(temperature),max(temperature),0.01))
pred4plot <- predict(
  severity.lm,
  xRange,
  level=0.95,
  interval="confidence"
)

Now, we'll calculate the confidence intervals for the origional data points and run a test to see if the points are inside the interval:

modelConfInt <- predict(
  severity.lm,
  level = 0.95,
  interval = "confidence"
)

insideInterval <- modelConfInt[,'lwr'] < severity[['diseasesev']] &
  severity[['diseasesev']] < modelConfInt[,'upr']

Then we'll do the plot- first a the high-level plotting function plot(), as you used it in your example, but we will only plot the points inside the interval. We will then follow up with the low-level function points() which will plot all the points outside the interval in a different color. Finally, matplot() will be used to fill in the confidence intervals as you used it. However instead of calling par(new=TRUE) I prefer to pass the argument add=TRUE to high-level functions to make them act like low level functions.

Using par(new=TRUE) is like playing a dirty trick a plotting function- which can have unforeseen consequences. The add argument is provided by many functions to cause them to add information to a plot rather than redraw it- I would recommend exploiting this argument whenever possible and fall back on par() manipulations as a last resort.

# Take a look at the data- those points inside the interval
plot(
  diseasesev~temperature,
  data=severity[ insideInterval,],
  xlab="Temperature",
  ylab="% Disease Severity",
  pch=16,
  pty="s",
  xlim=c(0,30),
  ylim=c(0,30)
)
title(main="Graph of % Disease Severity vs Temperature")

# Add points outside the interval, color differently
points(
  diseasesev~temperature,
  pch = 16,
  col = 'red',
  data = severity[ !insideInterval,]
)

# Add regression line and confidence intervals
matplot(
  xRange,
  pred4plot,
  lty=c(1,2,2),   #vector of line types and widths
  type="l",       #type of plot for each column of y
  add = TRUE
)

Answer 3

I liked the idea and tried to make a function for that. Of course it's far from being perfect. Your comments are welcome

diseasesev<-c(1.9,3.1,3.3,4.8,5.3,6.1,6.4,7.6,9.8,12.4)
# Predictor variable, (Centigrade)
temperature<-c(2,1,5,5,20,20,23,10,30,25)

## For convenience, the data may be formatted into a dataframe
severity <- as.data.frame(cbind(diseasesev,temperature))

## Fit a linear model for the data and summarize the output from function lm()
severity.lm <- lm(diseasesev~temperature,data=severity)

# Function to plot the linear regression and overlay the confidence intervals   
ci.lines<-function(model,conf= .95 ,interval = "confidence"){
  x <- model[[12]][[2]]
  y <- model[[12]][[1]]
  xm<-mean(x)
  n<-length(x)
  ssx<- sum((x - mean(x))^2)
  s.t<- qt(1-(1-conf)/2,(n-2))
  xv<-seq(min(x),max(x),(max(x) - min(x))/100)
  yv<- coef(model)[1]+coef(model)[2]*xv

  se <- switch(interval,
        confidence = summary(model)[[6]] * sqrt(1/n+(xv-xm)^2/ssx),
        prediction = summary(model)[[6]] * sqrt(1+1/n+(xv-xm)^2/ssx)
              )
  # summary(model)[[6]] = 'sigma'

  ci<-s.t*se
  uyv<-yv+ci
  lyv<-yv-ci
  limits1 <- min(c(x,y))
  limits2 <- max(c(x,y))

  predictions <- predict(model, level = conf, interval = interval)

  insideCI <- predictions[,'lwr'] < y & y < predictions[,'upr']

  x_name <- rownames(attr(model[[11]],"factors"))[2]
  y_name <- rownames(attr(model[[11]],"factors"))[1]

  plot(x[insideCI],y[insideCI],
  pch=16,pty="s",xlim=c(limits1,limits2),ylim=c(limits1,limits2),
  xlab=x_name,
  ylab=y_name,
  main=paste("Graph of ", y_name, " vs ", x_name,sep=""))

  abline(model)

  points(x[!insideCI],y[!insideCI], pch = 16, col = 'red')

  lines(xv,uyv,lty=2,col=3)
  lines(xv,lyv,lty=2,col=3)
}

Use it like this:

ci.lines(severity.lm, conf= .95 , interval = "confidence")
ci.lines(severity.lm, conf= .85 , interval = "prediction")