Ballistic curve problem

Question

Ok i know this is quite off-topic for programmers but still I need this for app, so here it is:

Ballistic curve (without wind or any other conditions) is specified by these 2 lines:

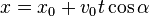
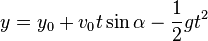
So, there is a problem that you got 3 unknown values: x,y and time t, but only 2 equations. You can't really compute all 3 with just these values, I got:

• velocity v
• angle Alpha
• origin coordinates

Thus, you have to decide which one to specify.

Now you have 2D tanks game, or anything like that, you know you have tank and using ballistic you have to shoot opponent down with setting angle and power.

I need to know when the bullet hit the ground, it can be on-air as it fly, or precomputed. There comes up my problem. Which way to use? Pre-compute or check for hitting the ground in each step.

If I would like to pre-compute, I would need to know height of terrain, which, logically would have to be constant as I don't know in which x coord. If I would know the X, it would mean that just in front of my turret is wall. So only way to get to result, when I hit the ground, would be with checking in intervals of time for hitting the ground. This is also good because the terrain doesn't have top be static yay! But isn't that too great overhead which could be made much simpler? Have you encountered with such problem/solution?

Thanks in advance, btw the terrain can be flat, using lines or NURBS so I please for general solution, not specific as in which height you shoot in that will be impact.

Answer 1

You can compute the path of the projectile y(x) by solving one equation for t and substituting into the other. You get

Then finding the landing point is a matter of computing the intersections between that function and the function that defines the height of the terrain. One intersection will be the launch point and the other will be the landing point. (If your terrain is very steep and hilly, there could be more than 2 intersections, in which case you take the first one with x greater than the launch point.) You can use any of various root-finding algorithms to actually compute the intersection; check the documentation of whatever mathematical or game-physical libraries you have to see if they provide a method to do this.

Answer 2

David Zaslavsky did a good job of answering your question about solving for the equation, but if your ultimate goal is simple ballistics simluation, I suggest you instead use vector decomposition.

By utilizing vector decomposition, you can derive the x- and y-compenent vectors of your projectile. You can then apply acceleration to each component to account for gravity, wind, etc. Then you can update the projectile's (x,y) position each interval as a function of time.

For example:

double Speed = 100.0;     // Speed rather than velocity, as it is only the magnitude
double Angle = 30.0;      // Initial angle of 30º
doulbe Position[2] = {0.0,0.0};  // Set the origin to (0,0)

double xvelocity = Speed * Cos(Angle);
double yvelocity = Speed * Sin(Angle);

Then if you can impliment a simple Update function as follows:

void Update(double Time)
{
     yvelocity = -9.8 * Time; // Apply gravity

     Position[0] *= (xvelocity * Time);  // update x position
     Position[1] *= (yvelocity * time);  // update y position

     CheckCollisions();  // check for collisions
}

Of course this is a very basic example, but you can build on it from here.