I have a a mesh, with certain types of elements (e.g. triangular, tetra). For each element I know all its vertices i.e. a triangular 2D element will have 3 vertices v1, v2 and v3 whose x,y,z coords are known.
Question 1
I am looking for an algorithm that will return all the edges... in this case:
edge(v1, v2), edge(v1, v3) , edge(v2, v3). Based on how many vertices each element has , the algorithm should efficiently determine the edges.
Question 2
I am using C++, so, what will be the most efficient way to store the information about the edges returned by the above algorithm? Example, all I am interested in is a tuple (v1, v2) that I want to use for some computation and then forget about it.
Thank you
You can use the half-edge data structure.
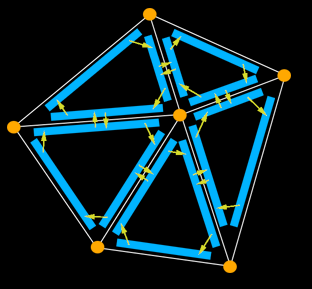
Basically your mesh also has a list of edges, and there is one edge structure per pair of verts in each direction. That means if you have verts A and B then there are two edge structures stored somewhere, one for A->B and one for B->A. Each edge has 3 pointers, one called previous, one called next and one called twin. Following the next and previous pointers walks you around the edges of the triangle or polygon in the mesh. Calling twin takes you to the adjacent edge in the adjacent polygon or triangle. (Look at the arrows int he picture) This is the most useful and verbose edge data structure I know of. I've used it to smooth meshes by creating new edges and updating the pointers. Btw, each edge should also point to a vertex so it knows where it is in space.
There are really three parts to your question, not two:
You have to ask additional questions to find appropriate answers.
What data structures should be used to represent the mesh?
What element types do you need to handle?
If you only need to handle polygons (closed loops) and simplicials (every node is connected to every other node in the element, such as a tetrahedron), then an ordered node list is sufficient because edges can be implied from the list of nodes. If, on the other hand, you need to handle element types such as hexahedra, prisms, or general polyhedra then you need more information about the element topology. A simple array of edge mappings is often sufficient. It's just an array[][2] of indices into the element's list of nodes which tells you how to connect the dots for a given element type.
The half-edge structure described by Chris is a good choice for 2D only. In 3D there can be an arbitrary number of elements attached to each edge, not just two. There is a 3D extension to the half-edge representation that I think is called a pinwheel structure.
If you've got to support arbitrary element types, I prefer a more complete data structure to represent element topology. A common option is to use edges and co-edges. There is an edge structure for each pair of connected nodes, and a co-edge for each use of that edge in an element. It's similar to the pinwheel approach, but a bit more explicit.
What algorithm should I use to extract edges from the elements?
How important is speed or memory? Should the result include each edge once per element, or only once no matter how many elements are using it? Does the order of edges in the result matter? Does the order of the nodes of each edge matter?
It's pretty hard to come up with an algorithm for arbitrary element types that will only visit each edge once. To ensure each edge only appears once, you can either filter the result, or you can be a bit hackish and keep a "visited" bit on each edge to ensure you don't stick it in the result twice.
How should I represent the results?
What matters about the way I will use the result?
If you're going to be using the result in a compute-intensive calculation, a big array of coordinates may be the best option. You don't want to re-fetch the node coordinates over and over during your computation. However, if you're filtering the results to remove duplicate edges, comparing coordinates (6 doubles for a node pair) is not the way to go. If you are filtering, generate a list of pointers to edge structures first, then filter out duplicates, and then generate your list of coordinates. You could use this approach with node pairs too, but then you have to filter against both possible node orders per edge, doubling the amount of time it takes to filter.
A list of edge pointers is also the way to go if memory matters more than performance. Instead of converting your edge list to a coordinate list, however, you look up coordinates during your calculation. Getting node coordinates is slower that way, but you avoid making a massive list of coordinates - you store a single pointer per edge instead of 6 doubles per edge.
Many mesh applications store all coordinates in a big global array, with each node having an index into the array. If this is the case, instead of converting your edge list to a coordinate array, convert it to a list of indices into the global coordinate array. Performance should not be much off from a local coordinate array, but without the memory and population overhead.
If you love us? You can donate to us via Paypal or buy me a coffee so we can maintain and grow! Thank you!
Donate Us With