Consider the given image of the soccer field

As you can see in the image the various ball movements, some of them are curved(i.e. in case of (1), (2), (3) in the image)) and some may not(i.e a line(4)),
so I need to find the intersection points of ball path with goalline and sideline. Sometimes the input may not be a curve(i.e a line) like in case of (4) given image
I have written a program, I have no clue what is wrong - is this right way to solve this kind of program.
if yes then, how to convert bezier curve into an equation for better solving
considering the given as
beizer curve eqaution -> a(x*x) + b*x + c
and line segment equation -> y = y1 + m(x-x1)
//maxCurvedPoint is the topmost of the curve
var getIntersectionPoint = function (room, ballFromPosition, ballToPosition, maxCurvePoint)
{
var linepoints = [[m1,n1], [m2, n2], [m3, n3], [m4, n4]];
//converting three points(ballFromPosition, maxCurvePoint, ballToPosition) into the quadratic equation (Bezier curve) --(1)
//getting the equation of the line segment using the linepoints --(2)
//equating (1) and (2) and getting a quadratic equation and solving and finding intersection points
return intersectionPoint;
}
// solves //(-b(+-)sqrt(b*b - 4ac)/2ac)
function solve(a, b, c)
{
//check curve intersects line or not
if((Math.pow(b, 2) - (4 * a * c)) >= 0)
{
result1 = (-1 * b + Math.sqrt(Math.pow(b, 2) - (4 * a * c))) / (2 * a);
result2 = (-1 * b - Math.sqrt(Math.pow(b, 2) - (4 * a * c))) / (2 * a);
return [result1, result2];
}
return [];
}
Can anyone help me with this? Also is the most curve point can be called vertex of the curve?
 asked Dec 07 '25 20:12
asked Dec 07 '25 20:12
I find it easier to work with vector equations since the algebra will be rotation-invariant (hence you don't have to re-write the code to deal with e.g. a "horizontal" parabola).
1. Curve representation + Intersection test
Consider a quadratic Bezier curve with endpoints A, C, control point B and parameter t:
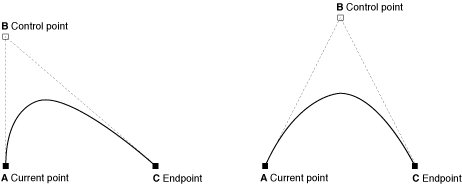

And an infinite line with source O, direction D and parameter s:

Equating P and R give a pair of quadratic simultaneous equations, which can be re-arranged to eliminate s and find the parabolic parameter t:

Solve this quadratic equation for t, and only accept real roots in the range [0, 1]. This ensures that any intersection point is always on the segment itself.
2. Dealing with line segments
You can also restrict the intersection point to a line segment, by computing s from t using the equations above, and limiting its value - which equals the distance along the line from O if D is normalized.
3. Computing the control point B
Note that a general value of the control point B will not give a symmetrical parabola. To compute B for a general symmetric curve:

Defining the variables:
M: midpoint of ABn: clockwise normal to the direction ACq: signed bulge distance - absolute value is the distance from M to the midpoint of the curvek: signed distance from M to B
A surprisingly simple result.
4. Sample C# (-style) code
public static Vector2[] computeIntersection
(
Vector2 A, Vector2 C, double q, // parabola segment
Vector2 O, Vector2 P // line segment
)
{
// quadratic solve
double[] solve(double a, double b, double c)
{
double d = b * b - 4.0 * a * c;
if (d < 0.0) // imaginary roots - no intersection at all
return null;
if (d > 0.0) // two distinct real roots
{
double sd = Math.Sqrt(d);
return new double[2] { (-b + sd) / (2.0 * a),
(-b - sd) / (2.0 * a) };
}
else // only one (line segment is tangent to curve)
{
return new double[1] { -b / (2.0 * a) };
}
}
// cross product (in-case undefined)
double cross(Vector2 i, Vector2 j)
{
return i.x * j.y - i.y * j.x;
}
// validity check for t and s
bool valid(double v)
{
return (v >= 0.0) && (v <= 1.0);
}
// compute control point B
Vector2 E = C - A;
Vector2 M = 0.5 * (A + C);
Vector2 N = (new Vector2(E.y, -E.x)).normalize();
Vector2 B = M + (2.0 * q) * N;
// solving for t
Vector2 D = P - O;
bool useX = Math.Abs(D.X) > Math.Abs(D.Y);
double[] T = solve(cross(A + C - 2.0 * B, D),
cross(B - A, D) * 2.0,
cross(A - O, D));
if (T == null) return null;
Vector2[] I = new Vector2[2];
int c = 0;
for (int i = 0; i < T.Length; i++)
{
// check if t is within curve range
double t = T[i];
if (!valid(t)) continue;
// solve for s and check if is within line range
double u = (1 - t) * (1 - t);
double v = 2 * t * (1 - t);
double w = t * t;
double s = useX ? ((u * A.X + v * B.X + w * C.X - O.X) / D.X)
: ((u * A.Y + v * B.Y + w * C.Y - O.Y) / D.Y);
if (!valid(s)) continue;
// compute the corresponding intersection point
I[c++] = O + s * D;
}
// only return valid solutions
if (c == 0) return null;
Array.Resize(ref I, c);
return I;
}
If you love us? You can donate to us via Paypal or buy me a coffee so we can maintain and grow! Thank you!
Donate Us With