I have a matrix eg.
[[4,5,0,0,0],
[5,1,2,1,0],
[0,2,3,2,0],
[0,1,2,1,0],
[0,0,0,0,0]]
For each element in the matrix, I am trying to get the sum of its adjacent diagonal elements and the sum of its adjacent horizontal and vertical elements.
Taking the 3 in the middle of the matrix for example, I am trying to calculate the sum of the diagonally adjacent elements (the 1's) and the horizontally and vertically adjacent elements (the 2's). For corner and edge cases, I want to disregard the areas where there are no elements eg.(for the 4 in the upper left, I'd want to get the sum of the diagonally adjacent 1 and the sum of the horizontally and vertically adjacent 5's.
What would be the most efficient way to do this in python?
So far i've come up with
diagonals = lambda x,y:[(x-1, y-1), (x-1,y+1), (x+1,y-1), (x+1,y+1)]
horiz_vert= lambda x,y:[(x,y+1), (x,y-1), (x+1,y), (x-1,y)]
to get the indices but these don't take into account the edge and corner cases.
 asked Oct 26 '25 04:10
asked Oct 26 '25 04:10
The right tool to solve this task appears to be convolution. You only need to define the filters that will be applied in each position ("sum of diagonal neighbors" or "sum of vertical/horizontal neighbors") and you're done.
import numpy as np
import scipy.signal
D = np.array([[4,5,0,0,0],
[5,1,2,1,0],
[0,2,3,2,0],
[0,1,2,1,0],
[0,0,0,0,0]])
h_diag = np.array([[1,0,1], [0,0,0], [1,0,1]])
h_hv = np.array([[0,1,0], [1,0,1], [0,1,0]])
Here's how the filters look like:
>>> h_diag
array([[1, 0, 1],
[0, 0, 0],
[1, 0, 1]])
>>> h_hv
array([[0, 1, 0],
[1, 0, 1],
[0, 1, 0]])
You can think of 2D convolution as of shifting the filter across your matrix and calculating in each position the sum of the element-wise multiplication. Strictly speaking, the filters need to be mirrored, but in your case they are symmetric anyway. Here's a random illustration of the principle as found on the web:
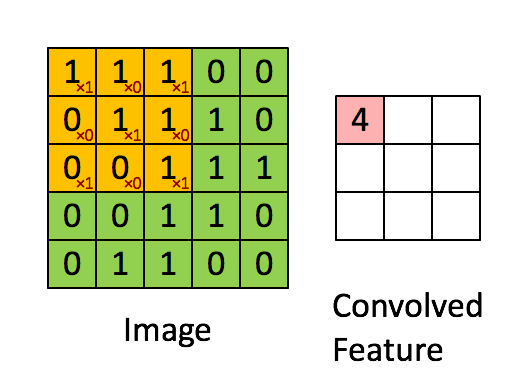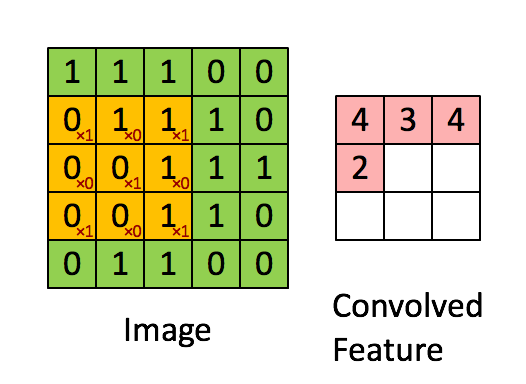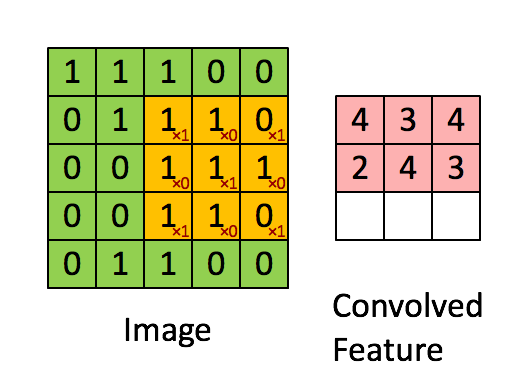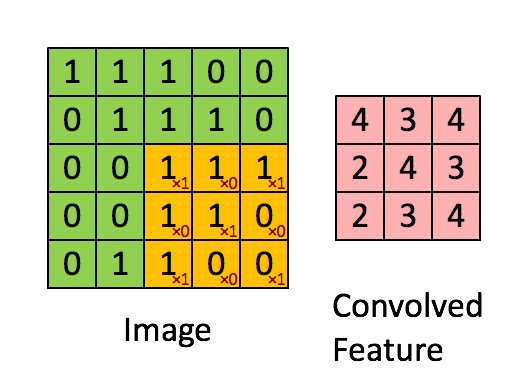
The only difference to your case is that we want to place the filters everywhere, including the "boundary" or "corner" positions. This can be achieved by zero-padding the original matrix D such that the center of the filter can be placed e.g. in position (0,0).
Good news! It's already implemented in Numpy/Scipy and it's a very efficient implementation! Now you just construct a matrix by convolving D with a filter h.
>>> scipy.signal.convolve2d(D, h_diag, mode='same')
array([[1, 7, 2, 2, 1],
[7, 7, 9, 3, 2],
[2, 9, 4, 4, 2],
[2, 3, 4, 3, 2],
[1, 2, 2, 2, 1]])
>>> scipy.signal.convolve2d(D, h_hv, mode='same')
array([[10, 5, 7, 1, 0],
[ 5, 14, 5, 4, 1],
[ 7, 5, 8, 5, 2],
[ 1, 4, 5, 4, 1],
[ 0, 1, 2, 1, 0]])
From these matrices you can read off the required sums in each position. E.g. the central element in your original matrix D, i.e. D[2,2] is surrounded by 4 ones on the diagonals and 4 twos on the horizontal/vertical adjacency. The entries in the convolution output at the position (2,2) are therefore 4 and 8. The position D[0,0] has only one diagonal neighbor (1) and two horizontal/vertical neighbors (5 and 5). The entries in the convolution output matrices are as expected 1 and 10.
If you love us? You can donate to us via Paypal or buy me a coffee so we can maintain and grow! Thank you!
Donate Us With