1/BigInteger in c#

Question

I want to make

BigInteger.ModPow(1/BigInteger, 2,5);

but 1/BigInteger always return 0, which causes, that the result is 0 too. I tried to look for some BigDecimal class for c# but I have found nothing. Is there any way how to count this even if there is no BigDecimal?

Answer 1

1/a is 0 for |a|>1, since BigIntegers use integer division where the fractional part of a division is ignored. I'm not sure what result you're expecting for this.

I assume you want to modular multiplicative inverse of a modulo m, and not a fractional number. This inverse exists iff a and m are co-prime, i.e. gcd(a, m) = 1.

The linked wikipedia page lists the two standard algorithms for calculating the modular multiplicative inverse:

• Extended Euclidean algorithm, which works for arbitrary moduli
  It's fast, but has input dependent runtime.

  I don't have C# code at hand, but porting the pseudo code from wikipedia should be straight forward.

• Using Euler's theorem:
  
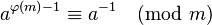
  This requires knowledge of φ(m) i.e. you need to know the prime factors of m. It's a popular choice when m is a prime and thus φ(m) = m-1 when it simply becomes 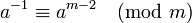. If you need constant runtime and you know φ(m), this is the way to go.

  In C# this becomes BigInteger.ModPow(a, phiOfM-1, m)